f:id:paiza:20191010173856p:plain — 主な確率分布の関連図

f:id:paiza:20151217152725j:plain こんにちは、吉岡（@yoshiokatsuneo）です。

Webサービスを運営していると、利用状況を分析・予測したり、A/Bテストなどで検証したりすることがよくあります。

データを一個一個見ていてもよくわからないので、データ全体や、その背景の傾向などがまとめて見られると便利ですよね。そんなとき、データの様子を表現するためによく使われているのが「確率分布」です。

学校の試験などで使われる偏差値も、得点を正規分布でモデル化して、点数を変換したものです。

今回は、Webサービスなどでよく使われる確率分布18種類を紹介します。

それぞれ、Webサービスでの利用例やPythonでグラフを書く方法も含めて説明していきます。コードは実際にオンライン実行環境paiza.IOで実行してみることができますので、ぜひ試してみてください。

【目次】

正規分布
対数正規分布
離散一様分布
連続一様分布
二項分布
多項分布
ポアソン分布
指数分布
ガンマ分布
幾何分布
負の二項分布
ベータ分布
ディリクレ分布
t分布
カイ二乗分布
F分布
コーシー分布
ロジスティック分布
まとめ

正規分布

f:id:paiza:20191010182511p:plain

# 正規分布, Normal Distibution
X=np.arange(-5, 5, 0.1)

fig, ax1 = plt.subplots()
ax2 = ax1.twinx()

ax1.plot(X, stats.norm.pdf(X, 0, 1), label='N(0, 1)')
ax1.legend();
ax1.set_ylabel('N(0,1)')
plt.ylim(0)
ax1.grid(axis='x')

ax2.plot(X, stats.norm.cdf(X, 0, 1), label='CDF', color='orange')
ax2.legend(loc='center right');
ax2.set_ylabel('CDF')
ax2.set_yticks(np.arange(0,1, 0.1))

plt.xticks(np.arange(X.min(), X.max(), 1))
plt.ylim(0)
plt.grid()
plt.show()

https://paiza.io/projects/7atgAI2mXNUffdyFhNHx6g

名称	正規分布(normal distribution), ガウス分布(Gaussian distribution)
記法	N(μ, σ²)
確率分布	$\displaystyle \frac1{\sqrt{2\pi} σ} exp \left( - \frac{{(x-μ)}^2}{2{σ}^2} \right)$
累積分布	$\frac{1}{2} \left( 1 + erf \frac{x-μ}{\sqrt{2{σ}^2}} \right)$ : $erf(x) = \frac{2}{\sqrt{π}} \int_{0}^{x} {e}^{-{t}^2} dt$
平均	μ
分散	σ²
共役分布	正規分布

たとえば、サイコロを何回か振っての出た目の和などは正規分布に当たります。　

正規分布は、確率分布の王とも言える有名な分布ですね。どんな分布でも足し合わせると正規分布になるという性質(中心極限定理)から、自然界でも社会でもあらゆる分野で広く存在しています。身長などの身体的特徴にあらわれることも多く、測定誤差はさまざまな要素が組み合わさったものなので、正規分布でモデル化することが多いです。

なお、正規分布の和も正規分布になり、平均も分散ももとの正規分布の和になります。

標準偏差は分散の平方根なので、精度を2倍(標準偏差を1/2)にするにはデータが4倍、精度を10倍にするにはデータが100倍必要になります。

Webサービスでは、日時アクセス数の分布(DAU)や、クリック数(CTR)、数が多い場合のA/Bテストの分布などで利用できます。

対数正規分布

f:id:paiza:20191011154958p:plain — 対数正規分布

# 対数正規分布, Log-Normal Distibution
X=np.arange(0, 5, 0.01)

fig, ax1 = plt.subplots()
ax2 = ax1.twinx()

for i, sigma in enumerate([0.5, 1, 2]):
    ax1.plot(X, stats.lognorm.pdf(X, sigma), label=f'Log Norm({sigma})')
    # ax1.axvline(x=math.e**(sigma**2/2), color=plt.get_cmap('tab10')(i)) # mean
    ax1.legend();plt.grid()
    ax1.set_ylim(0, 1.7)
    ax1.set_ylabel('Log Norm')

    ax2.plot(X, stats.lognorm.cdf(X, sigma), label=f'Log Norm CDF({sigma})', linewidth=0.5)
    ax2.legend(loc='center right'); plt.grid();
    ax2.set_ylim(0,1)
    ax2.set_ylabel('CDF')

plt.xticks(np.arange(X.min(), X.max(), 1))
plt.xlim(0, 5)
plt.show()

https://paiza.io/projects/nhNhQJivLYG_c8SH9T_d3Q

名前	対数正規分布(log-normal distribution)
確率分布	$\displaystyle \frac1{\sqrt{2\pi} σ x} exp \left( - \frac{{(\ln x-μ)}^2}{2{σ}^2} \right)$
累積分布	$\frac{1}{2} \left( 1 + erf \frac{x-μ}{\sqrt{2σ^{2}}} \right)$
平均	$e ^ {μ+\frac{σ^{2}}{2}}$
分散	$2^{2μ+σ^{2}} (e ^ {σ ^ 2} - 1)$
共役分布	正規分布

値の対数が正規分布になる分布です。

正規分布は左右対称ですが、グラフの右側に裾が長い場合、対数正規分布が利用できます。

年収の分布など、最低は0だけど、最高はどこまでも薄く続いていくような分布の場合に利用できます。

Webサービスでは、サービス滞在時間、投稿記事の長さなどが対数正規分布に従うことがあります。

離散一様分布

f:id:paiza:20191011160923p:plain — 離散一様分布

# 離散一様分布
X = np.arange(1, 7, 1)
Y = np.full(len(X), 1 / len(X))
plt.bar(X, Y)

https://paiza.io/projects/7fA7mUUEBAg5zhYS5Lh4jA

名前	離散一様分布(discrete uniform distribution)
確率分布	$\displaystyle \frac{1}{N}$
平均	$\frac{N+1}{2}$
分散	$\frac{N ^ 2 - 1}{12}$

サイコロを振った時に、1〜6のどの目が出るかなどの確率分布です。単純に、どの値も同じ確率の場合に使われます。

連続一様分布

f:id:paiza:20191011160811p:plain — 連続一様分布

# 連続一様分布(continuous uniform distribution)
a=0
b=10
X = np.arange(-5, 15, 0.1)
Y = np.where((X>=a) & (X <=b), 1/(b-a), 0)
plt.xticks(np.arange(X.min(), X.max(), 1))
plt.grid()
plt.ylim(0, 0.11)
plt.plot(X, Y)

https://paiza.io/projects/-bNPN-6XysujRM63G0eVxg

名前	連続一様分布(continuous uniform distribution)
記法	U(a, b)
確率分布	$\displaystyle \frac{1}{b - a}$ (a<=x<=b)
累積分布	$\frac{x - a}{b - a}$ (a<=x<=b)
平均	$\frac{a+b}{2}$
分散	$\frac{(b-a)^ 2 }{12}$

丸い鉛筆を転がしてどの辺りで止まるか？とか、プログラムの乱数などで使われる分布です。ベイズ統計の無情報事前分布としても使われます。

二項分布

f:id:paiza:20191011162428p:plain — 二項分布: Bi(10, 1/6)

f:id:paiza:20191011162502p:plain — 二項分布: Bi(20, 1/6)

f:id:paiza:20191011162533p:plain — 二項分布: Bi(30, 1/6)

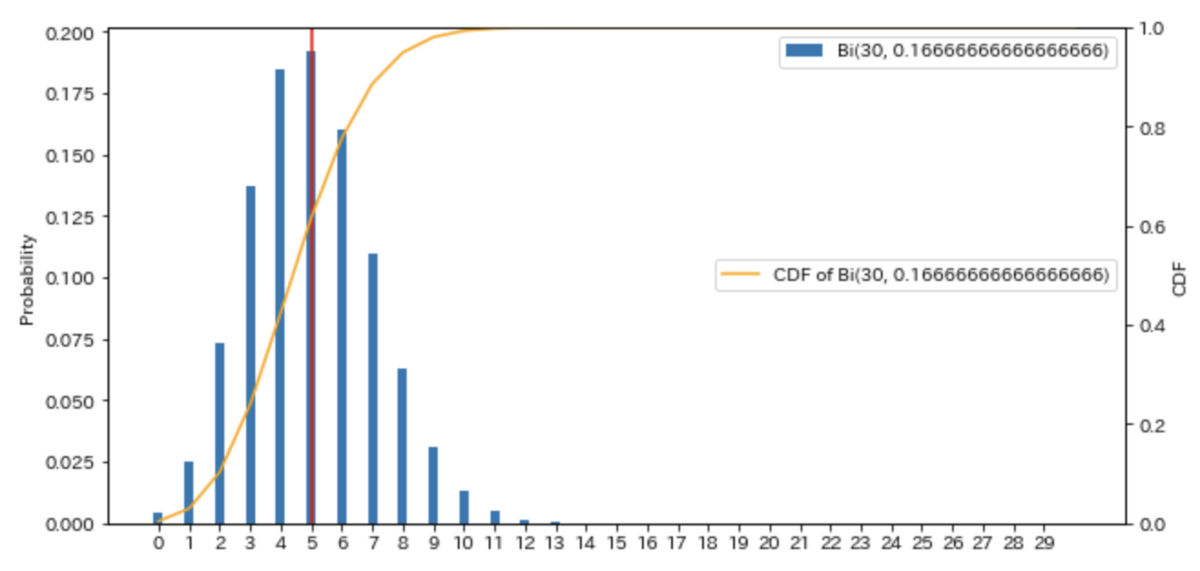
# 二項分布(Binominal Distribution)
p= 1/6
n=10
for n in [10, 20, 30]:
    X=np.arange(0, n+1)
    Y=[sp.special.comb(n, z)*p**z*(1-p)**(n-z) for z in X]
    fig, ax1 = plt.subplots()
    ax2 = ax1.twinx()
    ax1.bar(X, Y, label=f'Bi({n}, {p})', width=0.3)
    ax1.axvline(x = n*p, color='red')
    ax1.legend()
    ax1.set_ylabel('Probability')

    ax2.plot(X, np.cumsum(Y), label = f'CDF of Bi({n}, {p})', color='orange')
    ax2.set_ylim(0, 1)
    ax2.set_ylabel('CDF')
    ax2.legend(loc='center right')
    plt.xticks(np.arange(X.min(), X.max(), 1))
    plt.show()

https://paiza.io/projects/wOQUIrbEhB9k7Ce0XXM3ag

名称	二項分布(binomial distribution)
記法	Bi(n, p)
確率分布	$\displaystyle _ n C _ x p ^ x (1-p) ^{n-k}$
平均	np
分散	np(1-p)
共役分布	ベータ分布

同じコインを何回も振った時に、表が出る回数がこの分布です。表と裏の出る確率が同じなら、 p = 0.5 で左右対称な分布になります。コインの表裏のような、成功・失敗の２種類の結果が出るものをベルヌーイ試行と言います。

確立pで成功するベルヌーイ試行をn回行った時の分布が、二項分布 Bi(n, p)になります。

nが大きくなると、同じ平均・分散の正規分布N(np, np(1-p))で近似することができます。

nが大きくpが小さい場合、λ=npのポアソン分布で近似できます。

WebサービスでのA/Bテストも結果が2種類ですから、Aになる確率をp、Bになる確率を1-pとして、二項分布で表すことができます。

多項分布

名称	多項分布(multinomial distribution)
確率分布	$\displaystyle \frac{n!}{x1!...xk!} p _ 1 ^ {x _ 1}...p _ k ^ {x _ k}$
平均	$np_i$
分散	$np_i(1-p_i)$
共分散	$-n p_i p_j$
共役分布	ディリクレ分布

サイコロの1〜6の目のように、3種類以上ある場合、二項分布を拡張した多項分布で表すことができます。

k個の値をとる確率がp_1, ... ,p_kの試行を繰り返した場合の、それぞれの値が出る回数の分布が、n,pをパラメータとする多項分布になります。

Webサービスでは、3種類以上のLPを比較する場合などの、各LPへのアクセス数などで利用できます。

ポアソン分布

f:id:paiza:20191011163122p:plain — ポアソン分布: Po(1)

f:id:paiza:20191011163145p:plain — ポアソン分布: Po(2)

f:id:paiza:20191011163209p:plain — ポアソン分布: Po(3)

f:id:paiza:20191011163245p:plain — ポアソン分布: Po(4)

# ポアソン分布(Poisson Distribution)
for mu in [1, 2, 3, 10]:
    X=np.arange(0, 20, 1)
    Y=stats.poisson.pmf(X,mu)
    fig, ax1 = plt.subplots()
    ax2 = ax1.twinx()
    ax1.bar(X, Y, label=f'Po({mu})', width=0.3)
    ax1.axvline(x = mu, color='red')
    ax1.legend()
    ax1.set_ylabel('Probability')

    ax2.plot(X, np.cumsum(Y), label = f'CDF of Po({mu})', color='orange')
    ax2.set_ylim(0, 1)
    ax2.set_ylabel('CDF')
    ax2.legend(loc='center right')
    plt.xticks(np.arange(X.min(), X.max(), 1))
    plt.show()

https://paiza.io/projects/Jgvu5P6YFQqd67uOWKBfSg

名前	ポアソン分布(Poisson distribution)
記法	Po(λ)
確率分布	$\displaystyle \frac{λ^{k}}{k!} e^{-λ}$
平均	λ
分散	λ
共役分布	ガンマ分布

1時間に何人来客があるかなど、一定間隔で事象が発生する現象で使われます。

一定時間に平均λ回発生する事象が、k回発生する確率をあらわす分布です。λが10より大きい場合は、N(λ、λ)で近似することができます。

Webサービスでは、１日のコンバージョン数などで利用できます。

指数分布

# 指数分布(Exponential Distribution)
X = np.arange(0, 10, 0.01)

fig, ax1 = plt.subplots()
ax2 = ax1.twinx()

for l in [0.5, 1, 2]:
    ax1.plot(X, l * np.float_power(math.e, - l * X), label=f'Ex({l})')
    # ax1.axvline(x=1/l, color=plt.get_cmap('tab10')(i)) # mean
    ax1.legend();plt.grid()
    ax1.set_ylim(0, 1.7)
    ax1.set_ylabel('Probability')

    ax2.plot(X, 1 - np.float_power(math.e, - l * X), label=f'CDF Ex({l})', linewidth=0.5)
    ax2.legend(loc='center right'); plt.grid();
    ax2.set_ylim(0,1)
    ax2.set_ylabel('CDF')

plt.xticks(np.arange(X.min(), X.max(), 1))
plt.xlim(0, 5)
plt.show()

https://paiza.io/projects/DJc51tk4VT9HE3Ny4iYMiw

名前	指数分布(exponential distribution)
確率分布	$\displaystyle λ e ^{-λx}$
平均	$\frac{1}{λ}$
分散	$\frac{1}{λ^{2}}$

故障が起きるまでの時間などで利用されます。

単位時間あたり確率λで起きる事象が、発生するまでの時間の分布です。

Webサービスでは、サービスの解約率λが一定の場合、平均継続期間のコホート(ある時期に会員になったユーザ数)の推移などをあらわすことができます。

ガンマ分布

f:id:paiza:20191011165023p:plain — ガンマ分布

# ガンマ分布(Gamma Distribution)
X=np.arange(0,7,0.1)
for a in [1, 2, 3]:
    for b in [0.5, 1, 2]:
        plt.plot(X, stats.gamma.pdf(X, a, scale=1.0/b), label=f'Gamma({a}, {b})', color=plt.get_cmap('tab10')(a), linewidth=b)

plt.legend()
plt.ylim(0)
plt.xlim(0)
plt.show()

https://paiza.io/projects/_KXK5U64NFYD59_xHKy9hw

名前	ガンマ分布(Gamma distribution)
記法	Ga(α, λ)
確率分布	$\displaystyle \frac{λ^α}{Γ(α)} x^{α-1} e^{-λ x}$ ( Γ(α)はα!の一般化 )
平均	$\frac{k}{λ}$
分散	$\frac{k}{λ^{2}}$

指数分布を一般化した分布で、α=1で指数分布になります。単位時間あたり確率λで起きる事象が、α回発生するまでの時間の分布です。

Ga(n/2, 0.5)は自由度nのt分布になります。

幾何分布

# 幾何分布 (Geometric Distribution)
p=1/6

X=np.arange(1, 30)
Y=[p*(1-p)**(x-1) for x in X]
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
ax1.bar(X, Y, label=f'Geometric({p})', width=0.3)
ax1.axvline(x = (1-p) / p, color='red')
ax1.legend()
ax1.set_ylabel('Probability')

ax2.plot(X, np.cumsum(Y), label = f'CDF of Geometric({p})', color='orange')
ax2.legend(loc='center right')
ax2.set_ylim(0, 1)
ax2.set_ylabel('CDF')

plt.xlim(0)
plt.show()

https://paiza.io/projects/glo63SCX-Pa-elzLDdDIAg

名前	幾何分布(geometric distribution)
確率分布	$\displaystyle p (1 - p)^{x-1}$
平均	$\frac{1}{p}$
分散	$\frac{1-p}{p^{2}}$

コインを連続して振ったときに、何回目にはじめて表がでるかをあらわす分布です。指数分布の離散版になります。

確率pで起きる試行を成功させるまでの試行回数の分布が、パラメータpの幾何分布になります。

Webサービスだと、ある確率で広く拡散されるイベントが、何回目に実際に拡散されるかの分布をあらわせます。

負の二項分布

f:id:paiza:20191015112444p:plain — 負の二項分布: Be(1)

f:id:paiza:20191015141604p:plain — 負の二項分布: Be(2)

f:id:paiza:20191015141703p:plain — 負の二項分布: Be(3)

f:id:paiza:20191015141757p:plain — 負の二項分布 : Be(10)

# 負の二項分布(Binominal Distribution)
p=1/6
for k in [1,2,3,10]:
    X=np.arange(0, 60)
    Y=[sp.special.comb(k+x-1, x)*p**k*(1-p)**x for x in X]

    fig, ax1 = plt.subplots()
    ax2 = ax1.twinx()

    ax1.bar(X, Y, label=f'Be({k})', width=0.3)
    ax1.axvline(x = k * (1-p) / p, color='red')
    ax1.legend()
    ax1.set_ylabel('Probability')

    ax2.plot(X, np.cumsum(Y), label = f'CDF of Be({k})')
    ax2.legend(loc='center right')
    ax2.set_ylim(0,  1)
    ax2.set_ylabel('CDF')

    plt.xticks(X)
    plt.xlim(-1)
    plt.show()

https://paiza.io/projects/6-LdbEiZFIlOcFH_tokKVQ

名前	負の二項分布(negative binomial distribution)
確率分布	$\displaystyle _{k+x-1} C_x p^{k} q^{x}$
平均	$\frac{k}{p}$
分散	$\frac{k(1-p)}{p^{2}}$

幾何分布を一般化したものです。

コインを連続して振る時に、k回目の表がでるまで、何回裏が出る必要があるかをあらわす分布です。

確率pで起きる試行をk回成功させるまでの失敗回数の分布が、パラメータpの幾何分布になります。

Be(1)は幾何分布と同じです。二項分布の確率分布をP_b(x|n,p0)負の二項分布の確率分布を P_be(x|k,p)とすると、P_be(x|k,p) = P_b(k|x,p)となり、二項分布でパラメータと変数を入れて、二項係数を負に拡張した形になります。

Webサービスでは、ある確率で広く拡散されるイベントで、何回失敗すればk回目の拡散が得られるかをあらわす分布になります。

ベータ分布

f:id:paiza:20191015143401p:plain — ベータ分布

# ベータ分布(Beta Distribution)
for a in [0.5, 1, 2, 3]:
    for b in [0.5, 1, 2, 3]:
        x=np.arange(0,1,0.01)
        plt.plot(x, stats.beta.pdf(x, a, b), label=f'Beta({a}, {b})', color=plt.get_cmap('tab10')(a), linewidth=b)

plt.xlim(0, 1)
plt.ylim(0, 3)
plt.legend()
plt.show()

https://paiza.io/projects/kD3Ko8D9bzq1wxhoAtTXmg

名称	ベータ分布(beta distribution)
記法	Be(α、β), Beta(α, β)
確率分布	$\displaystyle \frac{ x^{α-1} (1-x)^{β-1} }{B(α, β)}$ : $B(α,β) = \int^{1}_0 x^{α-1} (1-x)^{β-1} dx$
平均	$\frac{α}{α + β}$
分散	$\frac{αβ}{(α+β)^{2}(α+β+1)}$

いびつな形のコインを振って表が20回、裏が10回出た場合に、そのコインの表がでる確率(事後確率)をBe(20-1, 10-1)で表すことができます。

Be(1,1)は一様分布で、二項分布の共役な分布になります。

ベイズ推定で、無情報事前分布での二項分布Bi(n, p)の結果がxの場合の、事後確率分布がBe(x+1, n-x+1)になります。

**Webサービスでは、ページに2つの選択ボタンがあり、それぞれAがα回、Bがβ回クリックされた場合の、AやBが選ばれる確率の分布で利用できます。

また、クリック率(CTR)などで、アクセスがNのページでクリックされた数がA、クリックされない数がB (=N-A)の場合の、クリック数の分布をBe(A+1, B+1)として表すこともできます。複数のLPがある場合なども、クリック率の分布を比較することでA/Bテストなどを行うことができます。**

ディリクレ分布

f:id:paiza:20191015161742p:plain — ディリクレ分布

# ディリクレ分布(Dirichlet Distribution)
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = fig.gca(projection='3d')

xx = np.zeros(shape=[99, 99])
yy = np.zeros(shape=[99, 99])
for a in range(0,99):
    for b  in range(0, 99):
        xx[b][a] = (a+1)/100.0 * (100-(b+1))/100.0
        yy[b][a] = (b+1)/100.0
        
a, b, c = (10, 3, 5)
di = stats.dirichlet([a+1, b+1, c+1])
Z = di.pdf([xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

xx2 = xx + (0.5 - xx.mean(axis=1).reshape(-1,1))
yy2 = yy * np.sqrt(3) / 2

ax.plot_surface(xx2, yy2, Z, cmap=matplotlib.cm.coolwarm)
plt.show()

https://paiza.io/projects/CUZI4_ZYRIxSAvyLnxNbQA

名前	ディリクレ分布(Dirichlet distribution)
確率分布	$\displaystyle \frac{1}{B(α)} \prod_{i=1}^{K} x_i^{αi-1}$
	ここで、 $B(α) = \frac{ \prod _ {i=1} ^ {K} Γ(αi) }{ Γ ( \sigma _ {i=1} ^ {K} α _ i) }$ , $\boldsymbol\alpha=(\alpha_1,\ldots,\alpha_K)$
平均	$\frac{α _i }{Σ _ k α _ k}$
分散	$\frac{α _ i(α _ 0 - α _ i)}{α _ 0 ^ 2(α _ 0+1)} : (α _ 0 = α _ 1 + ... + α _ k)$

ベータ分布は、コインの表裏のように2種類の場合に使いますが、サイコロの目のように3種類以上あるとき用に拡張された分布がディリクレ分布です。

サイコロを振って、1が10回、2が7回、3が4回、5が20回、6が15回出た場合に、そのサイコロでそれぞれの目が出る確率をDirichlet(10, 7, 3, 20, 6)と表すことができます。

Webサービスでは、たとえばページに4つの選択式ボタンがあり、それぞれ10回、5回、1回、20回クリックされた場合の、それぞれのボタンがクリックされる確率を表すことができます。

t分布

# ステューデントのt分布(Student's t distribution) / コーシー分布(k=1)
X=np.arange(-10, 10, 0.01)

for k in [1,2,3]:
    plt.plot(X, stats.t.pdf(X, k), label=f't({k})')

plt.plot(X, stats.norm.pdf(X, 0, 1), label=f'N(1,0)', color='black')

plt.legend()
plt.ylim(0)
plt.xlim(X.min(), X.max())
plt.show()

https://paiza.io/projects/Rq-nwcVGBB1D7xtZOmmCSw

名前	t分布、Studentのt分布 (Student's t-distribution)
記法	t(k)
確率分布	$\displaystyle \frac{Γ(\frac{ν+1}{2} )}{\sqrt{νπ} Γ(\frac{ν}{2})} \left( 1+\frac{x^{2}}{\nu} \right)^{-(\frac{ν +1}{2})}$
平均	0 (自由度kが1以下の場合は存在しない)
分散	$\sqrt{\frac{k}{k-2}}$ (自由度2以下の場合は存在しない)

5人がテストを受けて、得点が50,60,70,55,51点だった場合、得点の平均の分布は自由度(ν)4のt分布t(4)に従います。

平均μの正規分布に従うデータから、n個の実験データを抜き出した結果の標本平均をX, 標本分散をsの場合、 $T = \frac{X - μ}{\frac{s}{\sqrt{n}}}$ が自由度n-1のt分布t(n-1)に従います。

t分布は、自由度(ν)が大きい場合(30以上など)は正規分布で近似することができます。

また、2つの正規分布に従うデータに差があるか確認するt検定にも利用されます。

事前分布が一様分布で、尤度関数が正規分布の場合の事後分布もt分布になります。

誤差が正規分布の場合の線形な関係について、回帰分析の係数の分布は、自由度n-2のt分布 t(n-2) に従います。

自由度1のt分布はコーシー分布とも呼ばれます。

Webサービスでは、たとえばページの応答時間を5回測って、それぞれ0.8,1.0,0.9,0.7,0.7だった場合の平均応答時間の分布はt(4)に従い、応答時間の平均が95%信頼区間を求めたりすることができます。また、年齢とクリック率の相関係数の分布や検証にも使えます。

カイ二乗分布

f:id:paiza:20191015171722p:plain — カイ二乗分布

# カイ二乗分布(Chi-Square Distribution)
X=np.arange(0, 10, 0.01)
for k in range(1,10):
    plt.plot(X, stats.chi2.pdf(X, k), label=f'Chi({k})')
    plt.axvline(x=k, color=plt.get_cmap('tab10')(k-1), linewidth=0.5)
    
plt.ylim(0, 1)
plt.xlim(0, 10)
plt.legend()
plt.show()

https://paiza.io/projects/ZMJOmBgC4wWrt2hf-TRRtA

名前	カイ二乗分布、χ二乗分布(chi-square distribution, χ²-distribution)
記法	$χ ^ 2(k), χ ^ 2 _ k$
確率分布	$\displaystyle \frac{1}{2^{k/2}\Gamma(k/2)} x^{k/2-1} e^{-x/2}$
平均	k
分散	2k

60回サイコロを振ったとき、(1の目の数-10)/10 + .. + (6の目が出た数-10)/10は、自由度5(さいころの目の数6から1引いた数)のカイ二乗分布χ(5)に従います。

このサイコロに偏りがないか検定をおこなってみます。1が12回、2が13回、3が10回、4が9回、5が12回、6が5回出た場合、カイ二乗統計量は(12-10)²/10 + (13-10)²/10 + ... + (6-10)²/10 = 3.4 になります。自由度5のカイ二乗分布の上側確率P(χ²>3.4) = 0.6になり、60%の確率で起きることなので、このサイコロに偏りがあるとは言えません。

Z_1,Z_2..,Z_kが標準正規分布N(0,1)のときに、その二乗和 χ² = Z_1² + Z_2² + ... + Z_k² は自由度kのカイ二乗分布に従います。自由度kのカイ二乗分布の上側確率がαとなる値はχ²_α(k)と書きます。

適合度、独立性の検定などで利用されます。

Webサービスでは、A/Bテストで差があるかの検定に使われます。

F分布

# F分布(F Distribution)
X=np.arange(0, 5, 0.01)

for d1 in [1, 2, 10]:
    for d2 in [1, 2, 10]:
        plt.plot(X, stats.f.pdf(X, d1, d2), label=f'F({d1}, {d2})',  color=plt.get_cmap('tab10')(d1-1), linewidth=d2)    
plt.ylim(0, 1)
plt.xlim(X.min(), X.max())
plt.legend()
plt.show()

https://paiza.io/projects/SYAGmVuBYg_bFszNNAU7IQ

名前	F分布 (F-distribution)
確率分布	$https://wikimedia.org/api/rest_v1/media/math/render/svg/65803c3bdaed5d4c035f6366343875341620b203$
平均	$\frac{d2}{d2 - 2}$ (d2>2の場合)
分散	$\frac{2d_2^{2}(d_1 + d_2 - 2)}{d_1 ( d_2 - 2)^{2} (d_2 - 4)}$

2つの集団の分散が等しい場合、それぞれの標本数をm, n、標本分散をs_1, s_2とした場合、分散比F = s_1²/s_2²は自由度(m-1, n-1)のF分布　 F(m-1, n-1)に従います。

コーシー分布

f:id:paiza:20191015172731p:plain — コーシー分布

# コーシー分布
X=np.arange(-10, 10, 0.01)

plt.plot(X, stats.cauchy.pdf(X), label=f'Cauchy')

plt.plot(X, stats.norm.pdf(X, 0, 1), label=f'N(1,0)', color='black')

plt.legend()
plt.ylim(0)
plt.xlim(X.min(), X.max())
plt.show()

https://paiza.io/projects/quvulQPSUXW2P19NfOh02g

名前	コーシー分布(Cauchy distribution)、ローレンツ分布(Lorentz distribution)
確率分布	$\displaystyle \frac{1}{1+x ^ 2}$
平均	存在しない
分散	存在しない

t分布で自由度1の場合の分布です。平均も分散も存在しない、異端の確率分布です。平均が存在しないので、中心極限定理が成り立たず、足し合わせても正規分布になりません。

正規分布に比べて裾が厚いので、外れ値が発生する分布のモデルに使われます。

ロジスティック分布

f:id:paiza:20191015173125p:plain — ロジスティック分布

f:id:paiza:20191015173154p:plain — ロジスティック累積分布

# ロジスティック分布
mu = 0
s = 1
X = np.arange(-10, 10, 0.1)

Y = np.exp(-(X - mu)/s) / (s * (1+np.exp(-(X - mu)/s))**2)
plt.plot(X, Y, label='Logistic')
plt.plot(X, stats.norm.pdf(X, 0, (math.pi**2 * s**2 / 3.0)**0.5), label='N(0, pi^2/3)')
plt.grid(); plt.legend(); plt.ylim(0, 0.3)
plt.show()

Y = 1.0 / (1.0 + np.exp(-(X - mu)/s))
plt.plot(X, Y,  label='CDF Logistic')
plt.plot(X, stats.norm.cdf(X, 0, (math.pi**2 * s**2 / 3.0)**0.5), label='CDF N(0, pi^2/3)')
plt.grid(); plt.ylim(0, 1)
plt.legend()
plt.show()

https://paiza.io/projects/WGJwLHNIk_T2cI6uS8i62A

名前	ロジスティック分布(logistic-distribution) (累積分布: ロジスティック関数、シグモイド関数(sigmoid function))
確率分布	$\displaystyle \frac{e ^ {-(x-μ)/s}}{s(1 + e ^ (-(x-μ)/s)) ^ 2}$
累積分布	$\frac{1}{1 + e^{-\frac{x-μ}{s}}}$
平均	μ
分散	$\frac{π ^ 2}{3} s$

確率分布より、累積分布の方がよく使われているかと思います。累積確率分布がS字型で、0-1の値を返す関数で、分類などの用途で使われます。

関数値の比はオッズと呼ばれます。差が同じ値のオッズ(関数値の比)は同じになることから、強さをあらわすレーティングのモデルとしても使われます。

累積確率分布が、同じ平均・分散の正規分布に似ていることから近似として使われることもあります。

Webサービスでは、複数コンテンツの組み合わせでコンバージョンが発生する場合に、どのコンテンツの影響でコンバージョンするのか？などの多変量解析などで使われます。

まとめ

Webサービスの分析などで利用される、主な確率分析18種を紹介してみました。データ分析では、式や数字を見るだけでなく、グラフで見てわかることが多いですね。

確率分布についても、パラメータを変えながらいろいろなグラフを作って眺めると、より深く理解できますので、ぜひ試してみてください。

「PaizaCloud」は、環境構築に悩まされることなく、ブラウザだけで簡単にウェブサービスやサーバアプリケーションの開発や公開ができます。

「paizaラーニング」では、未経験者でもブラウザさえあれば、今すぐプログラミングの基礎が動画で学べるレッスンを多数公開しております。

そして、paizaでは、Webサービス開発企業などで求められるコーディング力や、テストケースを想定する力などが問われるプログラミングスキルチェック問題も提供しています。

スキルチェックに挑戦した人は、その結果によってS・A・B・C・D・Eの6段階のランクを取得できます。必要なスキルランクを取得すれば、書類選考なしで企業の求人に応募することも可能です。「自分のプログラミングスキルを客観的に知りたい」「スキルを使って転職したい」という方は、ぜひチャレンジしてみてください。