
Gerd AltmannによるPixabayからの画像
プログラミング学習をしていて「アルゴリズムを学びたい」という方は多いと思いますが、アルゴリズムの良し悪しを決める計算量についても合わせて理解しておく必要があります。
たとえば、競技プログラミングで問題を解く際に、計算量が少ないアルゴリズムを使って処理を高速化することは欠かせませんし、実務でも大規模なデータを扱う場合、計算量を考慮しないと要件を満たせないこともあります。
また複雑な計算処理を実行する機械学習の分野でも、高速化による計算効率の向上は欠かせません。
そこで今回は、計算量の基本について、初めて学ぶ方にも分かりやすく解説していきます。
そもそも「計算量」って?
計算量とは、簡単に言うと計算にかかるコストの指標です。計算量には空間計算量と時間計算量があります。
空間計算量は、プログラム実行時に使うメモリ量を指します。領域計算量と呼ぶこともあります。
時間計算量は、プログラムの処理時間を指します。処理が終了するまでに必要とする命令数はどのくらいかで見積もることができます。
今回は時間計算量について説明します。
「O(オーダー)」を理解しよう
オーダーを用いた計算量の考え方
時間計算量を表現する方法としてO記法(オーダー記法)というものが使われます。ランダウの記号とも呼ばれ計算量の上界*1を表します。
オーダーのスペルは「order」で、辞書を引くと「注文」や「順番」などの意味がありますが、計算量を語る上では「程度」や「等級」などの意味で使われています。
オーダーは、あるアルゴリズムがどれくらいの処理時間がかかるかを評価するものです。
具体的にはO(N) や O(N^2) といった形で表記され、それぞれ早くても計算量が n あるいは n^2 と同じぐらいで発散するという意味です。
発散という言い方をすると少し難しそうに感じますが、「無限大に向かって増えていく(いくらでも大きくなる)」と捉えていただくとよいかと思います。
Nであれば1から順に増えていき無限大に向かう。
N^2であれば1からNの2乗で増えていき無限大に向かう。
といった感じです。
オーダーで計算量を考えるときは、たとえば O(2n) や O(1/2 n^2) といった「2」や「1/2」の係数は省略され O(n) や O(n^2) と表記されます。細かい計算量を予想する必要がある場合、係数まで含めて考えることもありますが、実際の計算に対して支配的な項(係数を無視できるほど影響が大きい項)は 2n や n^2 になるためです。
オーダー表記の代表例
概念だけではちょっと分かりにくいので、代表的なものを紹介します。
| 記法 | 概要 |
|---|---|
| O(1) | 処理時間がデータの大きさに依存せず一定である。1回の処理で結果を得られる。 |
| O(logN) | 処理を行うたびにN個の処理対象が減っていく。データ量が増えてもほとんど処理時間が増えない。二分探索などが該当する。 |
| O(N) | 単純にN回ループするような処理。データ量の分だけ処理時間が増える。 |
| O(NlogN) | 上の2つを組み合わせたもの。二分探索をN個の対象すべてにおこなう場合など。クイックソート、マージソートなどが該当する。 |
| O(N^2) | 2重ループのこと。バブルソートのような工夫していないソートが該当する。 |
| O(N^3) | 3重ループのこと。行列計算などが該当する。 |
| O(2^N) | 2択問題をN問出したときのすべての組み合わせ数に一致。 |
| O(N!) | 巡回セールス問題でN箇所を順に回るときに最短になるルートを探す。すべての経路を計算することで最適解を得る。 |
これらがすべてではありませんが、代表例と言えばこのくらい知っていたらいいかなと思います。
O(2^N) や O(N!) といった指数部にNが出る計算量や階乗は指数関数時間のアルゴリズムと呼ばれます。今回挙げた中では、それ以外のものは多項式時間のアルゴリズムと呼ばれます。
グラフにすると分かりやすいので見てみましょう。

O(N!)がとんでもなく大きすぎて他がほぼグラフに現れていません…。これだとさすがに何がなんだか分からないので縦軸を対数スケールにしてみます。
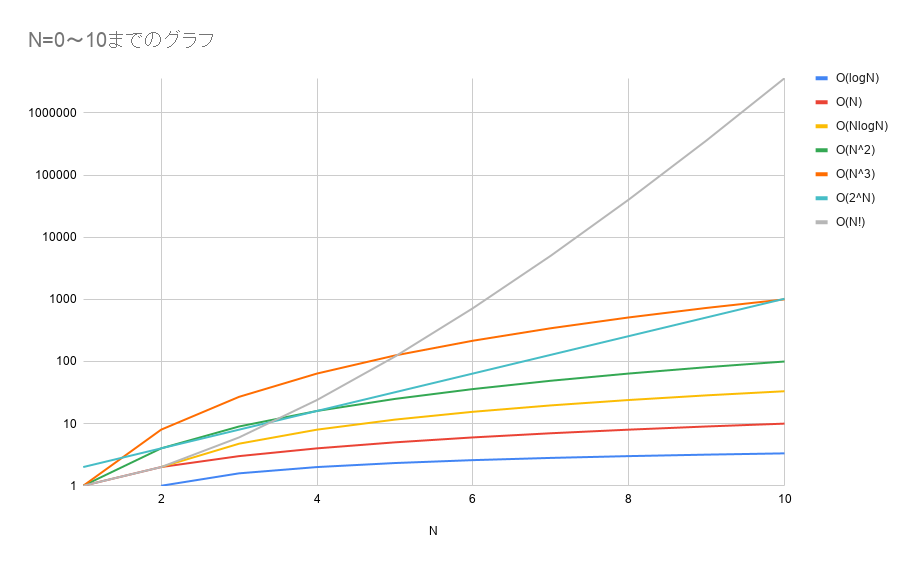
これでなんとなく比較できるようになりましたね。O(logN) から順に上がり方が大きいことが分かるかと思います。
また、O(N!) を見ると、Nが大きくなるにつれていかに計算量が増えていくかが分かります。
よく注目してみると O(2^N) と O(N^3) では、Nが10あたりで同じ計算量となっています。むしろNが10より小さい場合は、O(2^N) のほうが小さいです。上の表で例に挙げた、2択問題のすべての組み合わせを出すとき、実は8問程度であれば3重ループの方が計算量が大きいということが分かりますよね。
ただしこのままNを大きくしていくと…

このように O(2^N) も急激に計算回数が大きくなっています。グラフで見ると、指数関数時間の O(N!) や O(2^N) は、Nが大きくなると計算量が一気に大きくなってしまうことがよく分かります。
ここで指数関数時間の計算量はひとまず置いておいて、多項式時間のアルゴリズムの計算量だけを縦軸を対数目盛りから普通のグラフにもどして見てみましょう。

3重ループの O(N^3) も急激に計算量が増えていることが分かりますね。これらを実際N=1000で考えてみると…
O(N^3) は、3重ループなので10億回
O(N^2) は、2重ループなので100万回
O(N) は、そのまま1000回
O(logN) は、なんと9.96回程度!
となり二分探索などのアルゴリズムがどれだけ強力な手法かが分かります。
プログラミング問題で計算量を考慮する
ここまで計算量についてベースとなる知識をお伝えしてきましたが、実際のプログラミング問題ではどのように生きてくるのかを知るとより理解が深まると思います。
ここではpaizaラーニングの動画講座、「スキルチェック入門編2:日別訪問者数の最大平均区間 (Bランク)」を例に見てみることにします。
この講座では、1つの問題に対して3パターンの解き方を解説しています。計算量を考慮した解き方は「04:シンプルに問題を解く - その2」で取り上げています。
なお、講座で扱っている問題は「レベルアップ問題集」にて公開しています。時間制限なく何度でも解き直しも可能で、人と相談して解いても構いませんので学習に活用してみてください。
ちなみに講座のコードはPythonで書かれています。Pythonの基本文法から学びたいという方は「Python3入門編」(全編無料)をさきに受講していただくとスムーズです。
まとめ
計算量の基本的な考え方や代表的な例についてお伝えしてきました。
初心者のうちは計算量を考慮して処理を書くのは難しいと思いますが、まずは採用するアルゴリズム(処理の仕方)によってプログラムの計算量が大きく変わるということを知っておきましょう。
paizaでは、プログラミングスキルをS・A・B・C・D・Eの6段階で評価する「スキルチェック」を提供しており、スキルチェックのS・Aランク問題では、データ量が大きいテストケース(大規模データ)をパスできるかどうかも得点に影響します。
単純にループを回せば答えにたどり着ける問題もありますが、その場合大規模データでタイムアウトしてしまいます。そのため、この記事でお伝えしたように計算量を考慮して処理を書く必要があります。
スキルチェックは時間制限があり他の人と相談することはできませんので、プログラミング学習でどれくらい実力がついたかを試すのにはぴったりだと思います。
スキルチェックについて詳しくはこちら

これからプログラミング学習を始めたいという方には、paizaラーニングがおすすめです。Python、Java、C言語、C#、PHP、Ruby、SQL、JavaScript、HTML/CSSなど、プログラミング未経験者や初心者でも動画で学べる入門レッスンを公開しています。
「Python入門編」「C#入門編」「ITエンジニアの就活準備編」といった人気講座も完全無料となっておりますので、プログラミングを学びたい方・ITエンジニアを目指したい方はぜひごらんください。
詳しくはこちら

*1:実数の集合があるとき、その集合に属するどの数よりも小さくない数のこと。たとえば、xがAの上界というときは、すべてのAの要素aについてa≦xとなる。









