![]() こんにちは。paizaラーニングでコンテンツ制作をしている学生スタッフの工藤です。
こんにちは。paizaラーニングでコンテンツ制作をしている学生スタッフの工藤です。
以前、こちらの記事でソートアルゴリズムの基本について紹介しました。
今回はその続編として、もっと効率がよく実用的なソートアルゴリズムである「シェルソート」「マージソート」「クイックソート」を学べる練習問題集「効率的なソートアルゴリズムメニュー」を公開しました。
プログラミング問題を解いてソートアルゴリズムについてさらに理解を深めていきましょう!
なお、この問題集の一部の問題は「素朴なソートアルゴリズムメニュー」の内容を前提としているため、そもそもソートアルゴリズムとは何か?という前提を知りたい方、および「選択ソート」「挿入ソート」「バブルソート」に馴染みのない方は、まずそちらから取り組んでみてください。
レベルアップ問題集とは
「効率的なソートアルゴリズムメニュー」は、レベルアップ問題集にて公開しています。
レベルアップ問題集とは、プログラミング学習における計算ドリルや漢字ドリルのようなものだと思ってください。
ドリルのようにプログラミング問題を解き進めながら、解答例となるコード(一部言語)や解説文も参照できる*1ため分からないことを理解したり、苦手なポイントを克服したりできるように作られています。
paizaが提供しているスキルチェックとは異なり時間制限がなく、問題文や自分の解答コードを公開することが認められていますので、誰かと協力して取り組むことも可能です。
練習問題集「効率的なソートアルゴリズムメニュー」
「効率的なソートアルゴリズムメニュー」には、プログラミング問題が全3問用意されています。
ソートとは簡単に言うと、順序づけることができるデータの集まりを、なんらかの基準に従って並べる操作のことです。
ソート処理はとても基本的なアルゴリズムで、いたるところで利用されています。ほんの一例ではありますが、ソートを学習すると以下のことができるようになります。
- 得点表を元にしてランキングを作成する
- アドレス帳に登録した友人の情報を名前順に整理する
- データの集まりから上位k個のデータを取ってくる
- 貪欲アルゴリズムの前処理(参考:貪欲法 - Wikipedia)
など
出題される問題の特徴
ソートをおこなうためのアルゴリズムには多くの種類がありますが、このメニューでは冒頭でも挙げたとおり、その中でも効率がよく実用的なソートアルゴリズムとして知られている以下の3つを扱います。
- シェルソート
- マージソート
- クイックソート
ここでいう「効率がよい」というのはおもに「計算量が少なくて済む」ということを指しています。
少ないデータを対象にしたソートではそれほど違いはないかもしれませんが、大規模データをソートする際はアルゴリズムの良し悪しが処理速度に影響してきます。計算量について詳しくはこちらの記事も参照してみてください。
各問題では、ソートアルゴリズムの基本的な考え方を紹介したのち、疑似コードによる実装例を示しています。皆さんには実際にそのアルゴリズムを実装してもらい、アルゴリズムがどう動作するかを学習してもらいます。
なお、現在Python3、C++、Javaの解答コード例を用意しています。今後他の言語の解答コード例も追加予定です。
それでは実際に問題を見てみましょう。
1:シェルソート
問題文:
シェルソートは、挿入ソートを改良したアルゴリズムです。挿入ソートが整列済みのデータ列に強いことを利用しています。
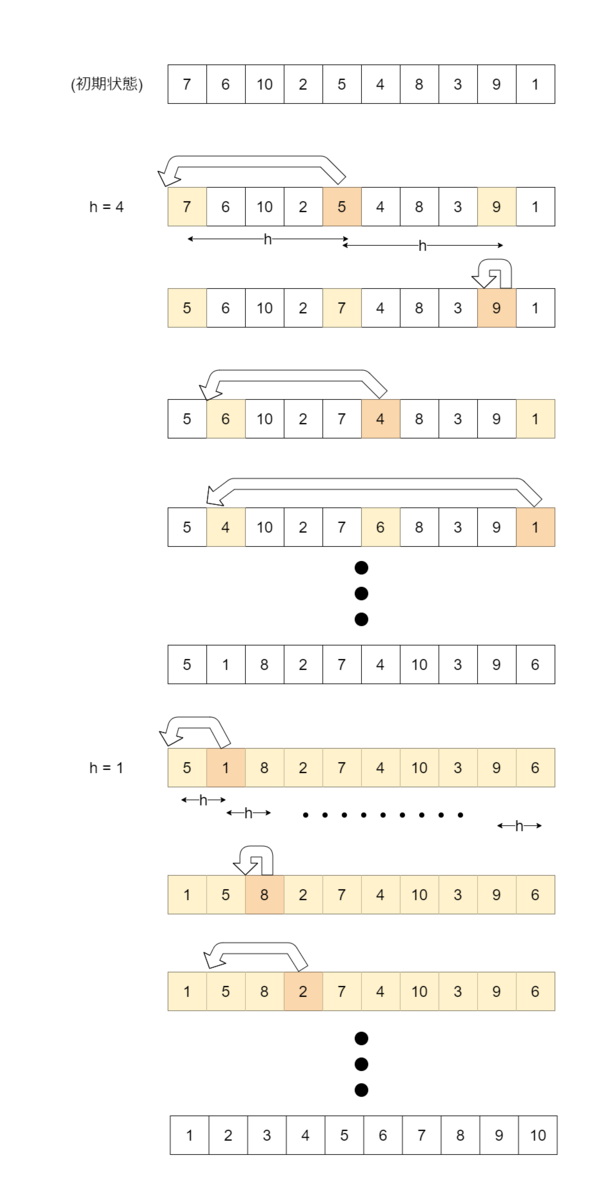
シェルソートでは、データ列において一定の間隔 h だけ離れた要素たちからなる部分列を対象とした挿入ソートを、h を小さくしながら (間隔を狭めながら) 繰り返してソートを行っていきます。h は適当に大きな値から始め、段階的に小さくしていき、最終的に 1 にします。h が 1 のとき、間隔が 1 離れた要素たちからなる部分列というのは元のデータ列そのものですから、このとき単純な挿入ソートを行うことになります。この時点でデータ列は既にほとんど整列済みとなっていることが期待されるため、ここで挿入ソートの強みが活かされます。
シェルソート (昇順) は以下のようなアルゴリズムです。
insertion_sort(A : 配列, n : Aの要素数, h : 間隔)
// アルゴリズムが正しく実装されていることを確認するために導入するカウンタ変数、ソート処理には関係がないことに注意
num_of_move <- 0
for i = h to n-1
// A[i] を、整列済みの A[i-ah], ..., A[i-2h], A[i-h] の適切な位置に挿入する
// 実装の都合上、A[i] の値が上書きされてしまうことがあるので、予め A[i] の値をコピーしておく
x <- A[i]
// A[i] の適切な挿入位置を表す変数 j を用意
j <- i-h
// A[i] の適切な挿入位置が見つかるまで、A[i] より大きい要素を後ろにずらしていく
while j >= 0 AND A[j] > x
A[j+h] = A[j]
j -= h
num_of_move++
// A[i] を挿入
A[j+h] <- x
shell_sort(A : 配列, n : Aの要素数, H : 間隔列)
for h in H
insertion_sort(A, n, h)
シェルソートの計算量は間隔列 H に強く依存します。シェルソートの計算量解析を正確に行うことは難しく、未解決です。いくつかの有名な間隔列に対しては計算量解析が行われており、例えば h_i = 3h_{i+1} + 1を満たす整数列 (..., 364, 121, 40, 13, 4, 1) を間隔列として採用した際のシェルソートは、平均計算量が O(n^{1.25}) になることが知られています。
では、要素数 n の数列を昇順にソートするシェルソートのプログラムを、上の疑似コードに従って実装してください。数列 h_1, ... , h_k が入力として与えられるので、それを間隔列として採用してください。なお、この数列は上で示した漸化式h_i = 3h_{i+1} + 1を満たしています。
アルゴリズムが正しく実装されていることを確認するために、各間隔 h_i について、num_of_move を出力してください。
入力される値:
n
A_1 A_2 ... A_n
k
h_1 h_2 ... h_k
- 入力はすべて整数
- 1行目に、数列の要素数 n が与えられます。
- 2行目に、数列の要素 A_1, A_2, ... , A_n が半角スペース区切りで与えられます。
- 3行目に、間隔列の要素数 k が与えられます。
- 2行目に、間隔列の要素 h_1, h_2, ... , h_k が半角スペース区切りで与えられます。
期待する出力:
k 行出力してください。
i 行目 (1 ≦ i ≦ k) には、間隔 h_i について、その処理が終わった時点での num_of_move の値を出力してください。
また、末尾に改行を入れ、余計な文字、空行を含んではいけません。
num_of_move
...
条件:
すべてのテストケースにおいて、以下の条件をみたします。
- 1 ≦ n ≦ 500,000
- -1,000,000,000 ≦ A_i ≦ 1,000,000,000 (1 ≦ i ≦ n)
- 1 ≦ k ≦ 12
- 1 ≦ h_i ≦ n (1 ≦ i ≦ k)
・ h_i は漸化式h_i = 3h_{i+1} + 1を満たす
・ h_k は 1
まずは説明文や図からシェルソートがどういったものかを理解してから、問題文中にある擬似コードを参考にして実装をしてみるとよいでしょう。
2:マージソート
つづいて、マージソートの問題です。
マージソート (昇順) は、データ列を二分し、それぞれをマージソートした後それらを「マージ (統合) 」することを繰り返すソートアルゴリズムです。マージソートは、問題を小さな問題に分割して解くことを繰り返すことによって元の問題の答えを得る手法である「分割統治法」に基づいたアルゴリズムです。
データ列を二分してマージソートを行う merge_sort と、昇順にソートされた2つの部分データ列をマージする merge から成ります。
マージソートも同様に問題文に説明や図を掲載しています。シェルソートとの違いを理解して、問題に挑戦してみましょう。
3:クイックソート
最後はクイックソートの問題です。
クイックソートは、ピボットと呼ばれる値を1つ選び、それを基準としてデータ列を「ピボット未満の要素からなるデータ列」と「ピボット以上の要素からなるデータ列」に二分することを再帰的に行うアルゴリズムです。
このアルゴリズムは、問題を小さな問題に分割して解くことを繰り返すことによって元の問題の答えを得る手法である「分割統治法」に基づいており、実用的なソートアルゴリズムの中で最も高速であるとされています (名前に quick と付いていることからも、その高速さが評価されていることが窺えます)。
ピボットの選び方にはいくつか種類があり、
- データ列の先頭をとる
- データ列の末尾をとる
- データ列からランダムにとる
- データ列からランダムに2つとり、その中央値をとる
等が例として挙げられます。今回は、2つ目の方法でピボットを選択することにします。
ピボットを選択したら、データ列の先頭からデータを1つずつ確認していき、ピボット未満のデータをデータ列の先頭に集めます。
そして、ピボットより左側がピボット未満、右側がピボット以上となるようにピボットを移動し、そこでデータ列を二分します。その後、分割された2つのデータ列に対して再び同じ操作を繰り返します。
少し複雑なので問題ページの図を見て理解するとよいでしょう。
ちなみにクイックソートは、データ列がバランスよくちょうど半分ずつに分割されていけば、データ列のサイズ n に対して約 log n 段にわたり分割がおこなわれることになり、最も効率よくソートすることができます。
データ列がバランスよく分割されるかどうかは、「ピボットの選び方とデータ列の相性」に強く依存しています。
さきほど計算量に少し触れましたが、クイックソートの平均計算量は O(n log n) であり、最悪計算量は O(n^2) であることが知られています。
まとめ
レベルアップ問題集に追加された「効率的なソートアルゴリズムメニュー」について紹介してきました。
アルゴリズムの学習にまだあまり取り組んだことがない方は最初は難しいと感じるかもしれませんが、掲載されている図や擬似コードを読み解くところから少しずつ始めてみましょう。
また、問題は擬似コードの改変で解けるようになっているため「以前勉強しようとしたけど挫折してしまった…」という方にもおすすめです。ぜひ、この問題集を使ってアルゴリズムの学習に挑戦してみてください。
プログラミング学習自体始めたばかりで問題集の内容が難しいと感じた方は、まずは基礎文法からしっかり身につけるのもよいでしょう。
paizaラーニングでは、Python・PHP・Ruby・Java・C・C#・JavaScriptなどの体験講座や入門講座を公開していますので、ぜひご活用ください。
練習問題をたくさん解いたあと、そろそろ自分のプログラミング力を腕試ししてみたい!という方は、時間制限ありのスキルチェックにもチャレンジしてみてください。
詳しくはこちら

*1:ただし、それらを閲覧するためには学習チケットが必要となります。チケットは毎日初回ログイン時に1枚付与され6枚まで所持できます。(有料会員の場合はチケットの消費なしで閲覧可能です)