![]() こんにちは。倉内です。
こんにちは。倉内です。
ある程度プログラミングの基本を学び終えた方の中には、アルゴリズムや数学的知識を深めたいという方もいらっしゃると思います。
paizaラーニングで公開している、プログラミング練習問題を集めた「レベルアップ問題集」では、アルゴリズムに関する問題集も多くご用意しています。
解答コード例や解説を誤用している問題も多数あるので、「アルゴリズムに興味はあるけど難しそうだし…」という方もぜひ挑戦してみてください。
今回はその中からグラフを扱った「グラフ構造の入力メニュー」「木のメニュー」をご紹介します。「グラフってそもそもなに…?」という方向けの説明もありますのでぜひ参考にしてみてください。
「レベルアップ問題集」とは
グラフについて考える前に、「レベルアップ問題集」がどんなものなのか少し説明しておきます。
この問題集はやさしい問題から順に解いていくことで、難しい問題(FINAL問題)まで段階的に理解を深めて、最終的には自力で解けるようになることを目指した作りになっているという特徴があります。
ここでいう難易度はpaizaが提供しているプログラミングスキルを測るサービス「スキルチェック」で出題される問題と対応しています。スキルチェックでは、S・A・B・C・Dランクに分けられた問題(Sがもっとも難しい)を決められた時間制限内に解く必要がありますが、レベルアップ問題集では時間制限はありません。
たとえば、「陣取りゲーム」というAランク相当の練習問題を解くには、C・B・Aランク相当の問題が順に用意されていて、最後に目的の問題を解けるようになっています。

レベルアップ問題集「Aランクレベルアップメニュー」より
レベルアップ問題集では、ループや条件文、配列といった基本文法をおさらいできる問題から、ソート、線形探索、などアルゴリズムに関する問題までさまざまな内容のものを公開しています。コードを書いて、実行して正誤判定まで、すべてブラウザ上でおこないます。
すべての問題の入力テストケースが参照でき、一部問題では解答コード例・解説もご用意しています。
グラフとは
グラフ構造
本題に入りますが、まずは「グラフ」が何かを説明したいと思います。プログラミングやアルゴリズムの勉強をしていてグラフと出てきたときは、大抵の場合はグラフというデータ構造のことを指します。
グラフとは、ノード(頂点)群とノード間の連結関係を表すエッジ(枝)群で構成される抽象データ型、および・またはその実装である具象データ型である。
グラフにもいくつか種類があります。たとえば、辺(エッジ、枝と同じ意味)に向きがつけられていない場合は「無向グラフ」といいます。下の図は、頂点の数が5の無向グラフの一例です。

今度は辺に向きがつけられている場合を見てみましょう。これは「有向グラフ」といいます。下の図は、頂点の数が5の有向グラフの一例です。

あとは辺に重み(コスト)がついている「重み付きグラフ」もよく見かけると思います。他に用語として知っておくとよいのはこのあたりでしょうか。
隣接…頂点同士が辺でつながっていること
接続…頂点と辺がつながっていること
閉路(cycle)…始点と終点が同じで、それ以外の頂点が異なるもの
自己ループ…辺の両端が同じ頂点であること
多重辺…辺の両端の頂点を同じくする辺が複数あること
多重辺というのは下の図のような状態を指します。
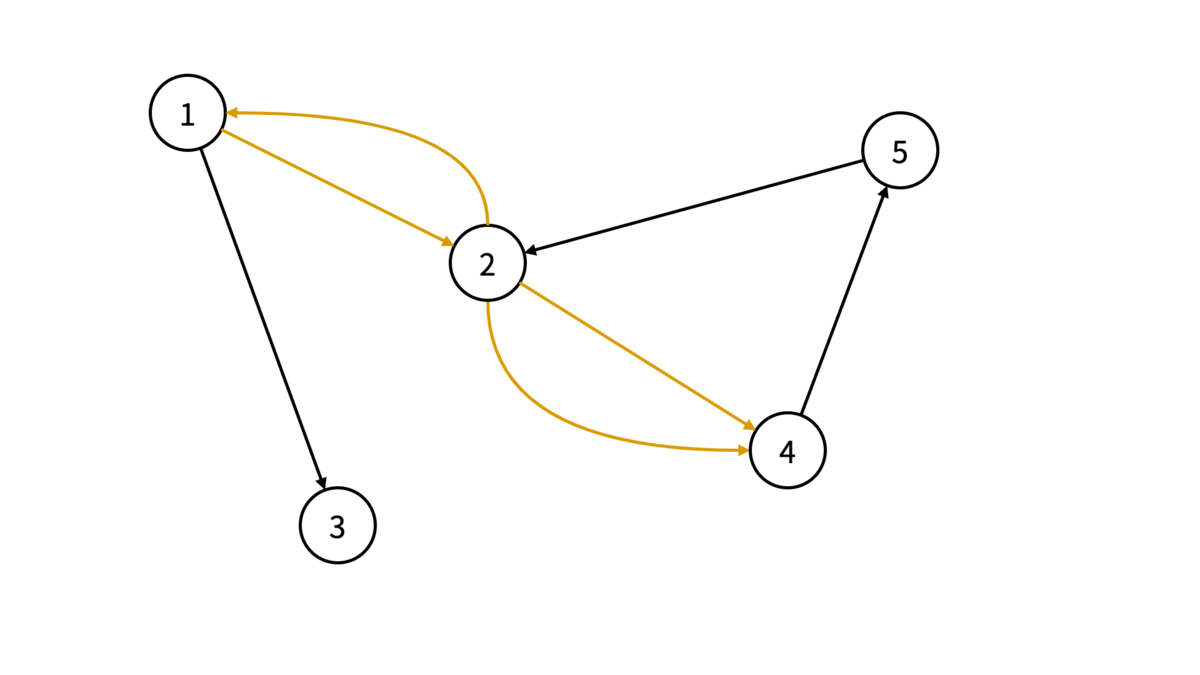
このように図にすると分かりやすくはありますが、実際に表現する際は「隣接行列」と「隣接リスト」のふたつがよく使われます。問題集にもこれらを学ぶ問題が出題されています。
例として、さきほど挙げた頂点の数が5の無向グラフを隣接行列で示してみます。1と2、1と3、2と4、2と5、4と5がつながっていましたよね。
ここでは縦5個、横5個の正方形型に5×5個の整数を並べて、上から1…5行目、左から1…5列目の要素を頂点と頂点が辺で直接つながっていれば 1、そうでなければ 0として表すことにします。

こうすることでプログラミングでも扱いやすくなりました。
(参考)木構造とは
データ構造のひとつに「木」というものがあります。たとえば、このような図で表すことができます。

木は閉路を持たない連結したグラフのことを言います。
問題集ではグラフ理論における木とはどういったものを指すか、図を用いて最初に説明がありますので、あまり馴染みがない方もぜひ挑戦してみてください。
グラフに関するアルゴリズム
グラフや木を探索*1するためのアルゴリズムに深さ優先探索(DFS:Depth First Search)や幅優先探索(BFS:Breadth First Search)があります。
それぞれ図を使って以下の記事で説明していますのでよければ参考にしてみてください。
それらの手法を使い、あるノードから別のノードへの最短経路を求める問題がよく出されます。最短経路問題で有用なアルゴリズムには、ダイクストラ法などがあります。
グラフを扱った練習問題に挑戦!
グラフがどういったものか分かったのでさっそく問題を解いてみましょう。
レベルアップ問題集の「グラフ構造の入力メニュー」および「木のメニュー」は、いずれもFINAL問題はA・Bランク相当となっています。
グラフ構造の入力メニュー
グラフの概念や知識を知らない人や難しいアルゴリズムを設計できない人にオススメのメニューです。グラフの入出力や隣接行列や隣接リストの実装ができるようになります。

こちらはB~Aランク相当の問題が用意されていますので、特にプログラミングの基本は習得していて、歯ごたえのある問題を解きたいという方におすすめです。
木のメニュー
グラフや木についての知識や扱いに自信がない人にオススメのメニューです。プログラミングにおいて木を扱う際の基本的な操作がわかるようになります。

「木のメニュー」では、まずはもっとも易しいDランク相当の問題から順に解いていく作りになっています。

一番最初の問題を実際に見てみましょう。
この問題集では、グラフ理論における木を扱います。
木とは、n 個の頂点と、それら全てを連結する n-1 個の辺からなるグラフのことです。
(図省略)プログラミングで木を扱う際には、辺の情報を利用しやすい形で保持することが好まれるので、隣接行列や隣接リストと呼ばれる形式で辺の情報を管理します。
この問題では、隣接行列を用いて辺の情報を管理してみましょう。グラフ (頂点数 N) の隣接行列とは、 N × N の行列 g であって i 行 j 列目の要素が
・ i 番目の頂点と j 番目の頂点が辺で結ばれているとき 1
・ 結ばれていないとき 0
であるようなもののことをいいます。木の頂点・辺についての情報が与えられるので、この木の隣接行列を出力してください。
実はさきほど例で示した、頂点の数が5の無向グラフの隣接行列が理解できていれば簡単に解けてしまいます。
だんだん難しくなるのですべてスムーズにはいかないかもしれませんが、自分がどのくらいのレベルであれば解けて、どのあたりから難しいかがよく分かります。ぜひじっくり取り組んでみてください。
もちろん腕試しをしてみたいという方は、いきなりA・Bランク相当の問題に挑戦しても構いません!
グリッド版ダイクストラ問題セット
さきほどグラフに関するアルゴリズムとして「ダイクストラ法」をご紹介しました。レベルアップ問題集では「グリッド版ダイクストラ問題セット」を公開しています。
グリッド上でダイクストラ法を活用して最短経路などを求める問題で、以下の記事で詳しい解説も公開しています。
その他のアルゴリズムの問題集
グラフから少し離れて、他のアルゴリズムを学べる問題集を紹介します。
ソート
ソート(sort)とは、昇順・降順・アルファベット順・日付順などのルールにのっとって、数値や単語といったデータを並べることを言います。
ソートアルゴリズムはたくさんありますが、シンプルな考え方である、挿入ソート、選択ソート、バブルソートあたりを学べるのが「素朴なソートアルゴリズムメニュー」です。
より実用的・効率的なソートである、シェルソート、マージソート、クイックソートを学べるのが「効率的なソートアルゴリズムメニュー」です。
いずれも問題はBランク相当ですが、問題ページにそれぞれのソートがどんなものなのか図を使いながら説明していますので、眺めてみるだけでもソートの理解が深まると思います。
探索(リスト・配列)
リストに入ったデータを探索する「線形探索」や「二分探索」は、さきほどの木を使ったのとは別のタイプの探索アルゴリズムです。
また、ハッシュ関数によって算出したハッシュ値を添え字としたハッシュテーブルを探索する「ハッシュ法」というのも探索アルゴリズムのひとつです。ハッシュ関数・ハッシュテーブルの実装ができるようになる問題集もあります。
ユークリッドの互除法
「ユークリッドの互除法メニュー」では、アルゴリズムの中でも定番の、最大公約数を求めるユークリッドの互除法や、その派生・関連アルゴリズムの知識がつきます。
実はユークリッドの互除法は記録に残っている最古(紀元前300年ごろ)のアルゴリズムと言われています。詳しくは以下の記事でも解説しています。
動的計画法
「DPメニュー」は、DP(Dynamic Programming、動的計画法)の問題を集めた問題集です。
DPとは、簡単に言うと、問題を部分問題に分割し、部分問題の答えを記録しながら、それらを利用することによって元の問題の答えを得る手法です。
この問題集では、Cランク相当の漸化式の問題を順に解いて、Bランク相当の問題を解けるように力をつけられます。
動画講座でアルゴリズムを学ぶ
paizaラーニングでは、「アルゴリズム入門編」という動画でアルゴリズムを学べる講座も公開しています。
さきほど動的計画法をご紹介しましたが、それの適用例の定番がフィボナッチ数列です。
他にも「ハノイの塔」や「巡回セールスマン問題」といった定番のアルゴリズムの解説をしています。アルゴリズムの基本として押さえておきたいものばかりですのでぜひチェックしてみてください。
まとめ
プログラミングの練習問題を集めた「レベルアップ問題集」の中から、グラフを使った問題集をはじめ、アルゴリズムに関する問題集をご紹介してきました。
アルゴリズムを学びたいと思ってもなかなか独学では「どう勉強していいか分からない…」と思っていた方はぜひレベルアップ問題集を活用してみてください!
なお、問題集の内容が難しいと感じた方は、まずは基礎文法からしっかり身につけるのもよいでしょう。
paizaラーニングでは、Python・PHP・Ruby・Java・C・C#・JavaScriptの7言語の入門講座を公開していますので、ぜひご活用ください。プログラミング言語入門講座一覧はこちら
paizaでは、paizaラーニングだけでなく、Webサービス開発企業などで求められるコーディング力や、テストケースを想定する力などが問われるプログラミングスキルチェック問題も提供しています。
スキルチェックに挑戦した人は、その結果によってS・A・B・C・D・Eの6段階のランクを取得できます。必要なスキルランクを取得すれば、書類選考なしで企業の求人に応募することも可能です。「自分のプログラミングスキルを客観的に知りたい」「スキルを使って転職したい」という方は、ぜひチャレンジしてみてください。
詳しくはこちら

*1:特定の制約条件を満たすものを見つけ出す行動のことで、特にプログラミングにおいては目的のデータがどこにあるかを探すという意味。