
Gerd AltmannによるPixabayからの画像
プログラミングにおけるアルゴリズムというと「正確に計算し、正しい結果を得るための効率のよい方法」といったイメージがありますよね。
このブログでもアルゴリズムに関する記事はいくつか書いてきましたが、単純ループだと時間がかかる処理をアルゴリズムを用いて計算量を減らそうとか、目的の値を効率よく探索しようとかそういった話が多かったと思います。
今回はこれまでとは少し違ったタイプの「乱択アルゴリズム」(ランダム・アルゴリズム、確率的アルゴリズムとも)というものを紹介したいと思います。
乱択アルゴリズムとは大雑把に言うと、乱数を使って平均するとよい結果を出せることを狙ったアルゴリズムを指します。
といってもこれだけでは分かりづらいので、数学や情報の授業などでもよく取り上げられる「モンテカルロ法」で具体的に説明していきます。Pythonでのコード例も示しますのでぜひご自分でも動かしてみてください!
乱択アルゴリズムの種類
乱択アルゴリズムには2種類あり、ひとつめが「ラスベガス法」と呼ばれるもの。もうひとつが冒頭で挙げた「モンテカルロ法」です。
ラスベガス法は、必ず正しい結果を返すか、あるいは計算に失敗したことを返すアルゴリズムです。運がよければ計算時間が短くなり、運が悪いと(可能性は低いが)計算時間が長くなります。
一方モンテカルロ法は、運がよければ短い計算時間で正しい結果を求めることができますが、運が悪いと間違った結果を返すアルゴリズムです。
アルゴリズムの説明で「運がよければ」というのはちょっと不思議な感じもしますが、ソートなどでもあらかじめの数字の並びで比較回数は変わったりするのでそう思うと納得できそうですね。
乱択アルゴリズムは、競技プログラミングの問題を解く際に利用することがあります。たとえば「多数あるものの中からひとつを見つける」「推定する(一部データの特徴から全体の特徴を予想する)必要がある」といった問題の場合などです。
書籍でいうと数学ガールシリーズが有名でしょうか。数学をテーマにストーリー仕立てで物語が展開していくため、とっつきやすいと思います。
2011年出版(電子書籍版は2014年)ですが、計算量についてていねいに書かれていて、今でもおすすめの書籍として挙げられることが多い1冊です。

- 作者:結城 浩
- 発売日: 2014/03/12
- メディア: Kindle版
乱択アルゴリズムの具体例
スライドパズルを完成させる
ここからはもう少し具体的に見ていきましょう。まずは、3×3のスライドパズルで考えてみます。
1から8までのパネルに数字が書かれていて、1箇所だけ空いています。はじめはバラバラになっていて、パネルをスライドさせて最終的に「左上から1から順に埋まって右下が空き」となればパズルの完成です。

このパズルを乱択アルゴリズムで解く場合、パズルのパネルがない領域と上下左右いずれかのパネルをランダムに入れ替え全部そろうまで繰り返します。
それでは実際にPythonでコードを書いてみましょう。ちなみに、Python3の基礎はpaizaラーニングの動画講座(全編無料)で学ぶことができます。
はじめの入力は以下のようにします。
876 543 21*
* をスライドパズルの空き領域とし、可能な限り短い手数で左上から1から順に埋まって右下が * となるように計算していきます。
from itertools import chain from random import choice from copy import deepcopy puzzle = [list(input()) for i in range(3)] #入力取得 def check(puzzle): #パズルが左上から順に並んでるかチェック return list(chain.from_iterable(puzzle)) == ['1', '2', '3', '4', '5', '6', '7', '8', '*'] def find_blank(puzzle): #パズルの * の位置を探す for i,v in enumerate(puzzle): for j,vv in enumerate(v): if vv == "*": return (i,j) move = [(1,0),(-1,0),(0,1),(0,-1)] #上下左右方向のリスト for i in range(5): #とりあえず5回試してみる puzzle_work = deepcopy(puzzle) #元のパズル盤面から今回処理する盤面をコピーする(2次元リストなのでdeepcopyしないと参照になるので注意 blank_xy = find_blank(puzzle) #パズルの * の位置を見つける cnt = 0 #手数記録 while check(puzzle_work) == False: #パズルが完成するまでループ move_tmp = choice(move) #上下左右方向を乱択する blank_move_xy = (move_tmp[0]+blank_xy[0], move_tmp[1]+blank_xy[1]) # * の位置に方向を加算 if 0 <= blank_move_xy[0] <= 2 and 0 <= blank_move_xy[1] <= 2: #方向がパズルの範囲内なら tmp_no = puzzle_work[blank_move_xy[0]][blank_move_xy[1]] #数字と * を入れ替えていく puzzle_work[blank_move_xy[0]][blank_move_xy[1]] = '*' puzzle_work[blank_xy[0]][blank_xy[1]] = tmp_no blank_xy = blank_move_xy # * の位置を移動 cnt += 1 #手数加算 print(puzzle_work,puzzle,cnt)
もっとも単純に実装したのが上記のコードです。
上に示した入力値でこのコードをpaiza.IO上で実行してみると…(タイムアウトする場合もあるので何度か実行してみてください)
[['1', '2', '3'], ['4', '5', '6'], ['7', '8', '*']] [['8', '7', '6'], ['5', '4', '3'], ['2', '1', '*']] 270660 [['1', '2', '3'], ['4', '5', '6'], ['7', '8', '*']] [['8', '7', '6'], ['5', '4', '3'], ['2', '1', '*']] 285056 [['1', '2', '3'], ['4', '5', '6'], ['7', '8', '*']] [['8', '7', '6'], ['5', '4', '3'], ['2', '1', '*']] 116910 [['1', '2', '3'], ['4', '5', '6'], ['7', '8', '*']] [['8', '7', '6'], ['5', '4', '3'], ['2', '1', '*']] 37818 [['1', '2', '3'], ['4', '5', '6'], ['7', '8', '*']] [['8', '7', '6'], ['5', '4', '3'], ['2', '1', '*']] 148278
何も考えず上下左右動かせる方向に動かしまくる処理になっているため、この書き方だと手数が数万~数十万という大変な結果になりました…。
今回は手順を見つけさえすれば正解としているので、運が非常に悪く計算時間をオーバーするとプログラムは停止し失敗となります。よってこの解法はラスベガス法と言えます。
こういった盤面の手順を決める乱択アルゴリズムは、将棋などの盤面ゲームのAIにも使われています。今の盤面から起こり得る盤面の運びを可能な限り計算し、勝利に近いほうを選んでいくというようなアルゴリズムです。
ただし、必ずよい手を取れるかというとそうではなく、悪い手を選んでしまうこともあります。
パズルと違って将棋などの場合は、最終的に求める答えは「勝つための一手」ですが、誤った答えを選ぶ可能性もあるためモンテカルロ法となります。
ちなみに過去に開催したPOH(paiza Online Hackathon)「僕の許嫁と幼なじみが修羅場すぎる」では、4×4のスライドパズルの問題を出題していました。以下の記事では乱択法での解法の一例を紹介しているのでよければ挑戦してみてください!
円周率の近似値を求める
モンテカルロ法は、ある値の近似を求めるといったことにも適しています。
定番の問題が円周率を求めるプログラムです。精度はそれほどよくありませんが、シンプルかつ円周率の性質を知っていると誰でもなるほどなと思えるアルゴリズムなので紹介します。
円の面積の公式は 半径×半径×円周率 です。今回は分かりやすく半径1の円で考えます。

円を4分の1にした弧で考えてみると、その面積は 半径×半径×円周率/4 となります。半径が1であれば円周率の4分の1となります。

この中心角90度の扇形を、1辺の長さが1、面積が1である正方形の中に入れてみます。そして、この正方形の中にランダムで点を打ち、その点が扇型の内側に入るか、外側に入るかを調べることで円周率を求めることができます。
ランダムに打った点が円の内側にあるか外側にあるかを確かめるには、円の方程式( x^2 + y^2 = 半径^2)を使います。今回は半径1の円なので x^2 + y^2 = 1 ですね。
(参考)円の方程式 | 数学II | フリー教材開発コミュニティ FTEXT
円の中心(扇型の要の部分)の座標を(0,0)、ランダムに打った点の座標を(x,y)として上記の公式へあてはめます。たとえば x=0.1, y=0.2であれば円の内側、x=0.6, y=0.8 であれば円の座標上、x=0.7, y=0.9であれば円の外側…というように、x^2 + y^2の値が、1以下か、1より大きいかで円の内側か外側かが決まります。
円の内側の点の数を打った点の総数で割り、円の内側の点の比率を求めます。これは半径1の円の4分の1の面積となります。
あとは結果を4倍するだけで円周率となります。コードは以下の通りです。
from random import random N = 100000 N_in = 0 for i in range(N): x,y = random(), random() if x**2 + y**2 <= 1: N_in += 1 print((N_in/N)*4)
とてもシンプルですよね。N=100,000とし10万個の点を打って円の内側か外側かを判断していって割り算をしているだけです。
10万個程度では3.14だったり3.15だったりとさすがに実用に耐えない精度ですが…。これがモンテカルロ法の「運がよければ」という部分ですね。逆に何度も実行してみると3.1416みたいにいい感じの値が出ることもあります。
当然Nを大きくすればするほど精度はよくなりますが、円周率を計算するアルゴリズムはもっとよいものがあるので、モンテカルロ法で求めるのはこのあたりにしておきます。
(参考)ガウス=ルジャンドルのアルゴリズム - Wikipedia
補足:作図して考えてみよう
ここまでの説明ではちょっとイメージがわきづらいかもしれないので、実際に画像に点を打って考えてみましょう。
以下のコードはpaiza.IOでは動かないため手元にPython環境がある方は動かしてみてください。PILというライブラリを使うので、もしインストールされていない場合は、pip install pillowというライブラリをインストールして実行してください。
from random import random from PIL import Image, ImageDraw IMAGE_SIZE = 500 img = Image.new('RGBA',(IMAGE_SIZE, IMAGE_SIZE)) img_draw = ImageDraw.Draw(img) img_draw.arc((-500, -500, 500, 500), start=0, end=360, fill=(255, 0, 0), width=12) img.save("base.png") N = 100 N_in = 0 for i in range(N): x,y = random(), random() if x**2 + y**2 <= 1: img_draw.arc((x*IMAGE_SIZE-3, y*IMAGE_SIZE-3, x*IMAGE_SIZE+3, y*IMAGE_SIZE+3),start=0,end=360, fill=(0,255,0), width=6) N_in += 1 else: img_draw.arc((x*IMAGE_SIZE-3, y*IMAGE_SIZE-3, x*IMAGE_SIZE+3, y*IMAGE_SIZE+3),start=0,end=360, fill=(0,0,255), width=6) print(N_in,N) print((N_in/N)*4) img.save("plot.png")
元のコードに円を描き、さらにランダムで点を決めて円の内側と外側で点を打つコードを追加しています。
赤い線が円、緑の点が円の内側、青の点が円の外側となっています。
10万個の点を打つと画面が埋め尽くされてしまうのでひとまず100個の点を打ってみます。もとの線は下図の赤い線です。

100個の点を打つと下図のようになります。
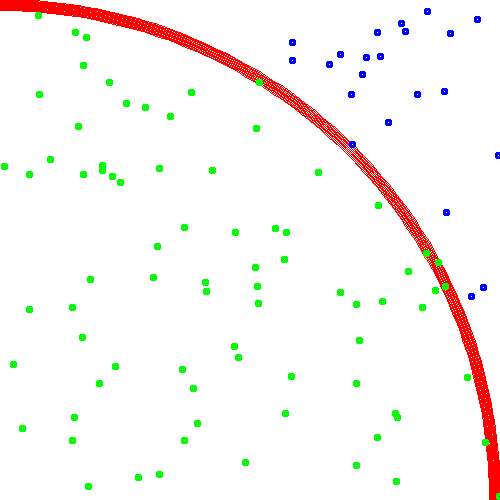
外側の点22個を数えれば全体100個に対して外側22個、内側78個と目視で数えられるでしょうか?
式に当てはめると 78 / 100 * 4 = 3.12 とそれっぽい値になります。これはわりと運がよかったときの例で、100個程度では 2.0 など大きくずれた値になる場合もあります。
20個の点にすると以下のようになり、内側・外側の点がそれぞれ目視で数えられるかと思います。
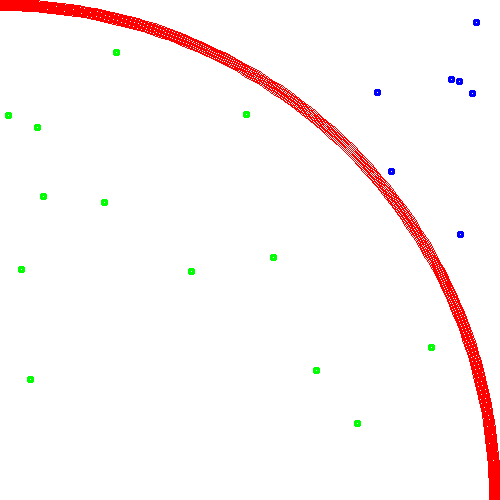
内側が13個、外側が7個、式に当てはめると 13 / 20 * 4 = 2.6 とだいぶ円周率から離れた値となりました。
イメージはつかめたでしょうか?点の数が大きくなればなるほど精度が上がっていくというのは、乱択アルゴリズムの試行回数を増やして実行時間が長くなればなるほどよい値になる確率が上がるというのと同じであることが分かりますよね。
まとめ
スライドパズルと円周率という身近な例を用いて、乱択アルゴリズムである「モンテカルロ法」を中心にお伝えしてきました。
名称だけ見ると小難しいものなのかなと思いがちですが、意外と理解しやすい内容だったなと思いませんか?
なんとなく数学に苦手意識があるという方でも、こんなふうに身近な例で考えたりしながらアルゴリズムを学んでみるとおもしろいかもしれません。
ちなみにpaizaラーニングでは、「アルゴリズム入門編」という学習講座を公開しています。フィボナッチ数やハノイの塔、巡回セールスマン問題といった定番のアルゴリズムが学べる内容となっていますので、興味がある方はぜひごらんください。
また、paizaが提供するプログラミングスキルを測るサービス「スキルチェック」では、特に難易度が高いS・Aランクの問題は計算量を考慮したコードを書く必要があります。アルゴリズムを勉強したあとは、ぜひそちらで腕試しをしてみてください。
「paizaラーニング」では、未経験者でもブラウザさえあれば、今すぐプログラミングの基礎が動画で学べるレッスンを多数公開しております。
詳しくはこちら







