
![]() こんにちは、吉岡([twitter:@yoshiokatsuneo])です。
こんにちは、吉岡([twitter:@yoshiokatsuneo])です。
Webサービスやアプリの開発時、新しいUIや機能と既存のものでどちらのほうがよいかを調べたいときにするのがA/Bテストです。
A/Bテストは、ユーザーなどのターゲットをランダムに半分(AとB)に分けて表示を切り替えて、それらのコンバージョン率(CVR)を比べることで効果を比較します。コンバージョン率(CVR)とは、例えばボタンなどがクリックされる割合(CTR)、商品が購入される割合、などのビジネス上の目標を達成できた割合です。
この方法は、A/Bをランダムに振り分けることからランダム化比較試験(RCT, Randomized Control Trial)とも呼ばれ、既存の方法を対象群(統制群, control group)、新しい方法を実験群(treatment group)と呼びます。
ランダム化比較試験は医療分野でも採用されている強力な方法です。最近はコロナウイルスのワクチンも、ランダム化比較試験での効果が確認されたことが承認につながりました。
(A/Bテストの結果の分析ではカイ二乗検定、二項検定などを使いますが、この評価方法については以下の記事で紹介しています)
このA/Bテストですが、どれくらいの期間行って、どれくらいのデータを集めれば信用に値する結果が出るのでしょうか。
「既存機能では一日100回クリックだったけど、新機能では200回になった」など、明らかな変化があればよいですが、データの量や効果が限られている場合はそんなに簡単にはいきません。
A/Bテストでどれくらいの期間、どれくらいの量のデータを集めればよいかを見積もるには、検定に必要なサンプルサイズ(標本サイズ)の計算を行います。
必要なサンプルサイズの求め方については、さまざまなケースがありますが、一般的にWebサービスのA/Bテストで検定を行う場合は、二項検定、カイ二乗検定のいずれかを使う場合が多いかと思います。
というわけで今回は、二項検定、カイ二乗検定での必要なサンプルサイズの求め方を紹介します。 あわせて、計算するためのPythonとRのコードや、ブラウザ上で簡単に計算できるページの紹介もします。
【目次】
- サンプルサイズの計算に必要な3要素
- 標本比率の確率モデル (コンバージョン率(CVR))
- 二項検定(1標本の比率の検定)のサンプルサイズの求め方
- カイ二乗検定(2つの比率の差の検定)でのサンプルサイズの求め方
- 参考
- まとめ
サンプルサイズの計算に必要な3要素
必要なサンプルサイズは、「A/Bテストを行うのに必要な日数は?」といったざっくりとした質問だけから求めることはできません。
サンプルサイズの計算には、どれぐらいの可能性で差があることにするか(有意水準)、どれくらいの可能性で差がないことにするか(検出力)、どれくらいの量の差があると考えるか(効果量)の3つが必要になります。

- 有意水準(significance, α):
A/Bで差がないとしたら、どれくらいの確率でこのような結果になるかを表します。
例えば、コインの裏表の場合、1回表は50%、2回連続表は25%、3回連続は12.5%、4回連続は6.25%、5回連続は3.125%で起こるので、有意水準を5%に決めると、5回連続表が出たときに「こんな偶然は可能性が低いので差がある」と判断します。
なお、この例は片側検定の場合で、一般的にはA>BとB<Aの二通りを考えて両側検定をするので、6回連続で有意となります。
有意水準を大きくすると必要なサンプルサイズは小さくなりますが、本当は差がないのに差があると判断する(第一種の過誤, Type-I error)の可能性が増えていきます。
一般的に5%が使われることが多いです。
- 検出力(検定力, power, 1-β):
差があるとすると、どれぐらいの確率で検定で「差がある」結果になるかを表します。
検出力が90%なら、1/10の確率で、本当は差があるのに「差がない」と判断してしまいます(第二種の過誤, β, Type-II error)。検定力を下げると必要なサンプルサイズは小さくなりますが、誤った結果を出す可能性は上がります。
一般的に80%が使われることが多いです。
- 効果量(effect size):
差があるとすると、どれぐらいの差があるかを表します。
例えば、CVRがA:5%B:6%の場合よりも、A:5%/B:7%のほうがAとBの差が大きいので、効果量も大きくなります。効果量が大きければ、小さいサンプルサイズでも結果が出ますが、効果量が小さいと大きいサンプルサイズでなければ効果がでません。
過去のデータ、予備実験、ドメイン知識、ビジネス上の最低限意味のある効果、などから期待する値を設定します。
有意水準、検定力を、真実と検定結果の表で表すと以下のようになります。
| 真実 | |||
|---|---|---|---|
| 無効(帰無仮説) | 有効(対立仮説) | ||
| 検定結果 | 無効(帰無仮説) | OK | β(第二種の過誤) |
| 有効(対立仮説) | α(有意水準,第一種の過誤) | 1-β(検定力) | |
なお、必要なサンプルサイズを有意水準・検定力・効果量から求める話をしましたが、この4つは3つを決めれば残りを決めることができます。例えば、測定できるサンプルサイズが決まっている場合、有意水準、検定力を決めると、効果量も求めることができます。
標本比率の確率モデル (コンバージョン率(CVR))
まず、測定したコンバージョン率(CVR)、つまり標本比率について確率モデルを立ててみます。
ページの表示回数をn, 実際のコンバージョン率(CVR)、つまり母比率をpとすると、コンバージョン回数 X は二項分布にしたがいます。
X 〜 B(n, p)
平均: np
分散: np(1-p)
二項分布 B(n,p) は 「nP >= 5 かつ n(1-p) >= 5」のときは正規分布N(np, np(1-p))で近似できます。
B(n, p) ≒ N(np, np(1-p))
次に、標本比率 p̂ について考えます。これは、コンバージョン回数を表示数で割ったものなので
と置けます。この平均、分散は以下の通りです。
したがって、p̂は以下の正規分布にしたがいます。
逆正弦変換(角変換)による近似
また、標本比率は逆正弦変換(角変換)を用いて近似することもできます。この場合、以下のように変換します。
サンプルに対しては、以下のように変換します。
p̂を変換した\hat{θ}は期待値をμとして、以下の正規分布にしたがいます。
ここで、には分散にpが含まれていない形になって計算しやすくなります。このような変換は、分散安定化変換とも呼ばれています。
二項検定(1標本の比率の検定)のサンプルサイズの求め方
同じページに2つのA/Bのボタンを表示するなど、A/Bの2つから1つが選ばれる場合について考えてみましょう。A/Bの2つからAを選ぶ比率の検定なので、検定は二項検定を使います。ここでは、この場合に必要なサンプルサイズの求め方を考えてみます。
計算方法
A/Bそれぞれの、コンバージョン率(CVR) を とします。
A/BからAが選ばれる確率(母標本比率)をpとすると、pは以下の通りです。
この測定結果 p̂は、正規分布にしたがいます。
分散を
と置くと
p̂ 〜 N(p, σ2)
となります。
したがって統計検定量として
を考えると、uは標準正規分布N(0,1)にしたがいます。
次に、帰無仮説(H0)について考えます。
このときpをとします。A/Bで違いがない場合、
となります。
このときの分散は
となり、統計検定量
は標準正規分布N(0,1)にしたがいます。
次に、対立仮説(H1)について考えます。
このときのpをとします。
このときの分散は
となり、統計検定量
は標準正規分布N(0,1)にしたがいます。
検定力は対立仮説(H1)のもとで、有意になる確率なので
これは以下のように変形もできます。 帰無仮説(H0)のもとでの有意水準を満たす境界値と、対立仮説(H1)のもとでの検定力を満たす境界値が等しいと考えれば自然です。
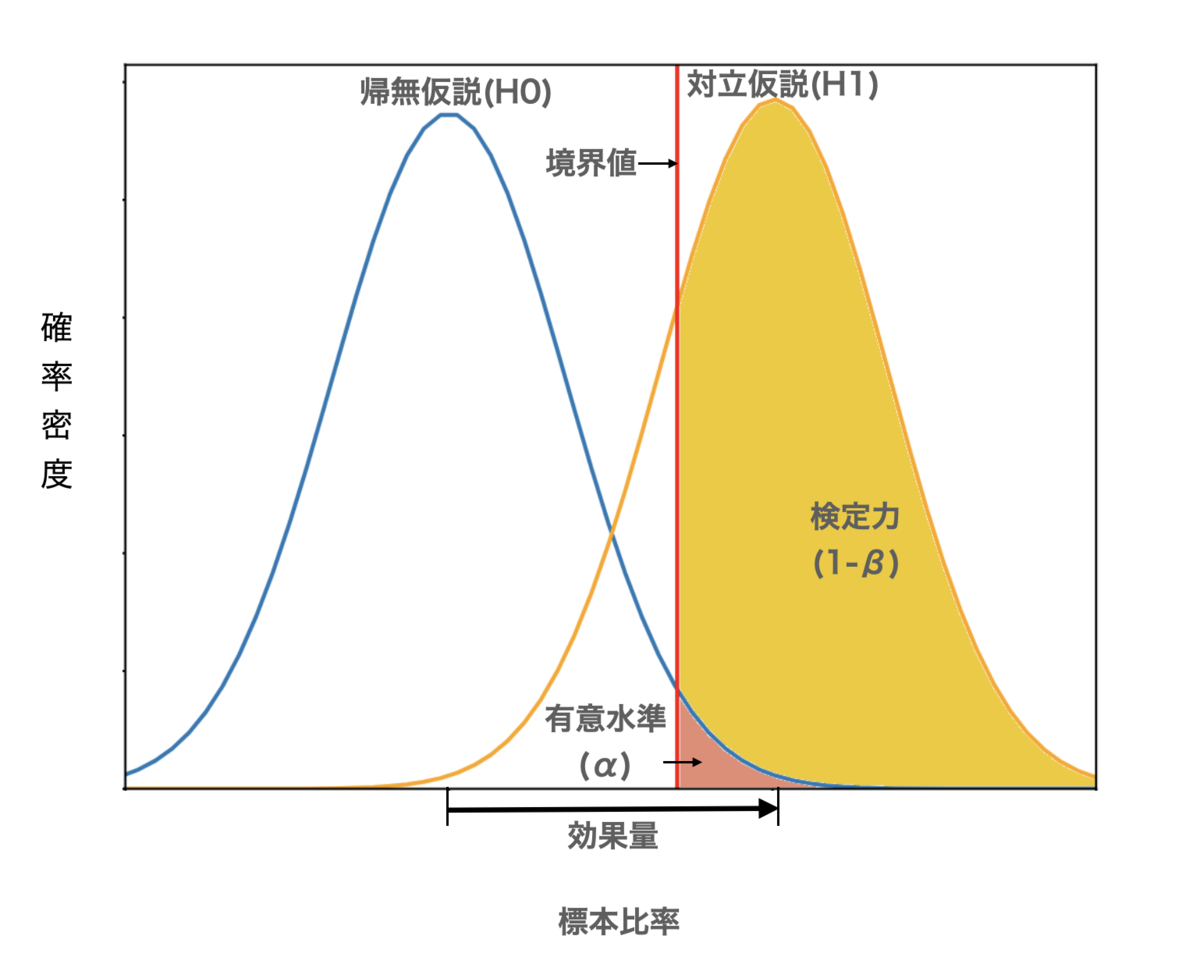
図で帰無仮説(H0)、対立仮説(H1)での標本比率の確率分布と、有意水準、効果量、境界値の関係を表すと、以下のようになります。
臨界値(境界値, critlcal value)は、H0で有意になる境界であり、かつH1で検定力が満たされる境界になります。
H0で臨界値より右側の面積がα(有意水準)、H1で境界値より左側の面積がβ(第二の過誤)・右側が検定力(1-β)になります。
これを変形すると、
となります。
A/Bのサンプルサイズを同じとすると
σ0, σ1を代入して解くと
となります。 なお、通常両側検定を考えるので、zαはzα/2となります。
簡易にp_0とp_1の平均を使って とするなら
で
となります。
さらに、有意水準5%、検定率80% (alpha=0.025, beta=0.2)とすると、zα=1.96, zβ=0.84で簡易的に
として計算できます。
逆正弦変換による近似
逆正弦変換による近似でも求めてみましょう。 この場合、同様に
となり
を代入して解くと
となります。
この結果は、 のみに依存しています。
はCohenのhと呼ばれ、効果量を示すのに使えます。同じhでは同じサンプル数になります。
このhを使うと、nはシンプルに
とかけます。
計算例
実際に計算してみましょう。
ここでは、例えば同じページにA/Bのボタンをおいた場合に、Aがクリックされる確率について考えます。 何も差がない確率を50%、差がある場合の確率を60%としてみます。(p_0=0.5, p_1=0.6) また、有意水準5%(α=0.05(片側検定で0.025))、検定力80%(1-β=0.8)として、必要なサンプルサイズnを計算してみます。
Python(式で計算)
(https://paiza.io/projects/mH-9_yvv7W8TjYGbRZNOtA)
R(式で計算)
(https://paiza.io/projects/e0qJsUZfu9zJ6cR2wBv1CA)
R(式で計算) (逆正弦変換)
(https://paiza.io/projects/D2yZ9WCIXNkrzsLgsw3t3w)
R(pwr.p.test)
Rでは、pwr.p.testを使って以下のようになります。
library(pwr) pwr.p.test(n=NULL, ES.h(0.5, 0.6), sig.level=0.05, power=0.8)
https://paiza.io/projects/Dga4ex3yt-Va57DykOmIng
なお、n以外の値をNULL以外にして、ほかのいずれかをNULLにすることで、サンプルサイズから効果量(h)・有意水準(sig.level)・検定力(power)を求めることもできます。
Python(statsmodels.stats.power.NormalIndPower.solve_power)
Pythonでは、statsmodels.stats.powerの、NormalIndPower().solve_powerが利用できます。
statsmodels.stats.powerの、NormalIndPower().solve_power
import statsmodels.stats.power as smp print(smp.NormalIndPower().solve_power(effect_size=0.2013579, alpha=0.05, power=0.8, alternative='two-sided', ratio=0))
193.58391309026072
(https://paiza.io/projects/SND6oL9R45Nx19CFwVnQBQ)
Web上で計算
以下のサイトでは、Web上で簡単に、効果量(p_0・p_1)・有意水準・検定力、から検定に必要なサンプルサイズを計算できます。
二項確率の仮説検定に基づくサンプルサイズ設計 | Kengo Nagashima - Keio University

確率分布
帰無仮説(H0), 対立仮説(H1)での標本確率(p0, p1)の確率分布を見てみると、以下のようになります。 臨界値(境界値, critlcal value)は、H0で有意になる境界であり、かつH1で検定力が満たされる境界になります。
H0で臨界値より右側の面積がα(有意水準)、H1で境界値より左側の面積がβ(第二の過誤)・右側が検定力(1-β)になります。

https://paiza.io/projects/e/QWm3_p79Qq8r1kM_MgHdJw
カイ二乗検定(2つの比率の差の検定)でのサンプルサイズの求め方
A/Bの二種類のページをランダムに表示し、どちらがよりコンバージョン率(CVR)が高いか調べる場合を考えます。このような2つの比率の差の検定には、カイ二乗検定やフィッシャーの正確検定を使います。この場合に必要なサンプルサイズを求めてみましょう。
計算方法
A/Bそれぞれのコンバージョン率(CVR)(母比率)をとすると、標本比率は正規分布で表せます。
A/Bの差を考えるとこれは正規分布の差になり、正規分布の差も正規分布で平均・分散は以下の通りです。
平均: E(X-Y)=E(X)-E(Y) 分散: V(X-Y)=V(X)+V(Y)
したがって、標本比率の差の分布は以下のように表せます。
ここで
と置きます。
次に、帰無仮説(H0)について考えます。 この時のpをp_0とします。A/Bで違いがない場合、p_0=0となります。 この時の分散は、n_a = n_b = nとし、またプールした比率
を用いて
となり、統計検定量
は標準正規分布N(0,1)にしたがいます。
次に、対立仮説(H1)について考えます。 この時のpをp_1 = p_b - p_aとします。 この時の分散は n_a = n_b = nとして
となります。
統計検定量
は標準正規分布N(0,1)にしたがいます。
二項検定の場合と同様に、H0での有意水準の境界値とH1での検定力の境界値が等しいことから
これをnについて解くと
となります。
より簡単に、 と近似すると
となります。
さらに、有意水準5%、検定率80% ()とすると、
となり、簡易的に
として計算できます。これは
ともかけるので、簡易に標準偏差の4倍が標本比率の差になります。
逆正弦変換による近似
また、二項検定の場合と同様、逆正弦変換で求めることもできます。
この場合、以下のように近似できます。
この差について考えると
帰無仮説(H0)のとき、、つまり
なので
対立仮説(H1)のときは
これまでと同様に、H0での有意水準の境界値と、H1での検定力の境界値が等しいことから
これを変形すると
を代入すると、
nについて解くと
この結果は、 のみに依存しています。
はCohenのhと呼ばれ、効果量を示すのに使えます。同じhでは同じサンプル数になります。
このhを使うと、nはシンプルに
とかけます。
これは1標本の場合の二倍になります。
計算例
それでは、求めた式やライブラリを使って、実際に計算してみましょう。
ここでは、既存の標本比率(コンバージョン率(CVR))を10%()、新機能の標本比率を15%(
)、有意水準5%(α=0.05(片側検定で0.025))、検定力80%(1-β=0.8)として、必要なサンプルサイズnを計算してみます。
Python(式で計算)
Pythonで計算すると、以下のようになります。
(https://paiza.io/projects/wCRET4PwcuHvyuWHyj19AQ)
R(式で計算)
Rで計算すると、以下のようになります。
(https://paiza.io/projects/gWbCGu7iog1yviJp9kpbQw)
R(power.prop.test)
Rではpower.prop.testを使うと、以下のように求められます。
> library(pwr) > power.prop.test(n=NULL, p1=0.1, p2=0.15, sig.level=0.05, power=0.8) Two-sample comparison of proportions power calculation n = 685.5969 p1 = 0.1 p2 = 0.15 sig.level = 0.05 power = 0.8 alternative = two.sided NOTE: n is number in *each* group
https://paiza.io/projects/fgomskLx7NrsLCYBhUAsSA
なおn以外の値をNULL以外にして、ほかのいずれかをNULLにすることで、サンプルサイズから比率(p1, p2)・有意水準(sig.level)・検定力(power)を求めることもできます。
R(pwr.2p.test)
Rでは、pwr.2p.testを使うと以下のように求められます。(逆正弦変換の利用)
pwr.2p.test ( source )
> library(pwr) > pwr.2p.test(n=NULL, ES.h(0.1, 0.15), sig.level=0.05, power=0.8) Difference of proportion power calculation for binomial distribution (arcsine transformation) h = 0.1518977 n = 680.3527 sig.level = 0.05 power = 0.8 alternative = two.sided NOTE: same sample sizes
https://paiza.io/projects/jCBjCBDxoAGc0O7OWdhv0g?
なおn以外の値をNULL以外にして、ほかのいずれかをNULLにすることで、サンプルサイズから効果量(h)・有意水準(sig.level)・検定力(power)を求めることもできます。
Python(statsmodels.stats.power.normal_sample_size_one_tail)
Pythonではstatsmodels.stats.power.normal_sample_size_one_tailを使うと以下のように求められます。
statsmodels.stats.power.normal_sample_size_one_tail ( source )
import math from statsmodels.stats.power import normal_sample_size_one_tail p1 = 0.1 p2 = 0.15 p = (p1 + p2) / 2 std = math.sqrt(2 * p * (1 - p)) print(normal_sample_size_one_tail(diff=p1 - p2, power=0.8, alpha=0.05 / 2, std_null=std, std_alternative=std,))
https://paiza.io/projects/RrWnMNN3hZRnFl-NXphyIw
Web上で計算
以下のサイトでは、Web上で簡単に、効果量(p_a・p_b)・有意水準・検定力、から検定に必要なサンプルサイズを計算できます。
2 x 2 分割表のカイ二乗検定に対するサンプルサイズ設計 | Kengo Nagashima - Keio University

シミュレーション
シミュレーションで検定力を確認してみます。
> foo = function(n) { n1 = rbinom(1, n, 0.1) n2 = n - n1 n3 = rbinom(1, n, 0.15) n4 = n - n3 fisher.test(matrix(c(n1,n2,n3,n4), nrow=2))$p.value } > p = replicate(10000, foo(685)); mean(p <= 0.05) [1] 0.7821
https://paiza.io/projects/_Hlb0ZKQ8SuCjiR6YWLqjw?
およそですが、検定力が0.8近くになっています。
確率分布
帰無仮説(H0), 対立仮説(H1)での標本確率(p0, p1)の確率分布を見てみると、以下のようになります。 臨界値(境界値, critlcal value)は、H0で有意になる境界であり、かつH1で検定力が満たされる境界になります。
H0で臨界値より右側の面積がα(有意水準)、H1で境界値より左側の面積がβ(第二の過誤)・右側が検定力(1-β)になります。

https://paiza.io/projects/e/QWm3_p79Qq8r1kM_MgHdJw
参考
サンプルサイズの決め方 (統計ライブラリー) | 永田 靖 |本 | 通販 | Amazon (p.165「母不良率の検定」、p.173「母不良率に関する一元配置分散分析」)
検出力を計算する方法【適切なサンプルサイズで検定しよう!】 | シグマアイ-仕事で使える統計を-
http://blue.zero.jp/yokumura/workshop/2010b/effectsize_power.pdf
統計的仮説検定における効果量の概念と必要サンプルサイズの算出|Dentsu Digital Tech Blog|note
まとめ
A/Bテストを必要十分な期間・量で行うには、テストに必要なサンプルサイズを求める必要があります。必要なサンプルサイズを求めるには、有意水準(例: 5%)、検定力(例: 80%)、効果量(例: 10%=>15%)の3つの項目が必要です。
サンプルサイズが小さすぎると、本当は効果があっても「効果がない」と判断してしまうことになりますし、大きすぎても、無駄なテストによって機会損失が生じてしまいます。適切なサンプルサイズを求めて、適切なA/Bテストを実施し、データに基づいた改善を進めましょう。
「PaizaCloud」は、環境構築に悩まされることなく、ブラウザだけで簡単にWebサービスやサーバアプリケーションの開発や公開ができます。

 「paizaラーニング」では、未経験者でもブラウザさえあれば、今すぐプログラミングの基礎が動画で学べるレッスンを多数公開しております。
「paizaラーニング」では、未経験者でもブラウザさえあれば、今すぐプログラミングの基礎が動画で学べるレッスンを多数公開しております。
詳しくはこちら
そしてpaizaでは、Webサービス開発企業などで求められるコーディング力や、テストケースを想定する力などが問われるプログラミングスキルチェック問題も提供しています。
スキルチェックに挑戦した人は、その結果によってS・A・B・C・D・Eの6段階のランクを取得できます。必要なスキルランクを取得すれば、書類選考なしで企業の求人に応募することも可能です。「自分のプログラミングスキルを客観的に知りたい」「スキルを使って転職したい」という方は、ぜひチャレンジしてみてください。
詳しくはこちら




