プログラミング問題を解けばエンジニアの戦闘力がわかる！？レーティング機能公開

f:id:paiza:20151217152725j:plain こんにちは、吉岡(@yoshiokatsuneo)です。

paizaでは、S・A・B・C・Dと5つのランクにわかれたプログラミングスキルチェック問題を公開しています。

スキルチェック問題を解いてこのランクを獲得することで、paizaでは、最初の書類選考なしで求人応募ができるようになっています。

paizaは、ユーザーのプログラミングスキルをより正確に評価できる方法を探し続けており、今回、「エンジニア戦闘力」「レーティング」という数字でスキルを可視化する方法を実験的に取り入れることになりましたので、どのようなものかご説明していきます。

※記事公開時（2019/09/10）はβ版として「エンジニア戦闘力」という数値も用いていましたが、2019/11/21公開の正式版では「レーティング」に統一されました。

スキルランクの課題について

従来のスキルランクはわかりやすいのですが、場合によっては以下の課題も出てきます。

同じランクの人同士の違いがわからない
同じランクの問題でも難しさが違う
Sランクをとってしまったらそれ以上がない
複数問題を解いていてもランクが上がらないと可視化されない

今回、「エンジニア戦闘力・レーティング」の機能では、これらの課題に以下のように対応しています。

数字でスキルを可視化する(100, 1000, 10000など)
問題の難しさも、同様に数字で可視化する(100, 1000, 10000など)
チャレンジしたすべての問題の結果を反映する
過去にチャレンジした問題について、エンジニア戦闘力・レーティングの変化をグラフで可視化する

エンジニア戦闘力・レーティングの表示

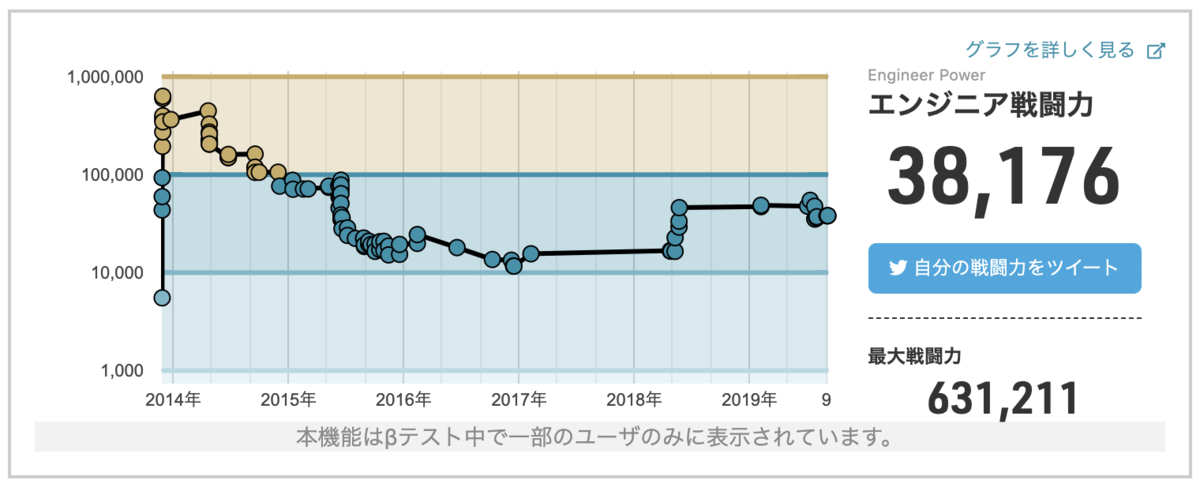
スキルチェックのページでは、以下のようにスキルを表す数字、過去の最大値、今までの履歴が表示されます。

※まだ実験段階の機能ですので、ユーザーアカウントによって「エンジニア戦闘力が表示される」「レーティングが表示される」「何も表示されない」が変わります。しばらくこのテストを実施したのち、改めて表示形式を改善する予定ですので、何も表示されていない方もいらっしゃるかと思いますがご了承ください。

「エンジニア戦闘力」として表示
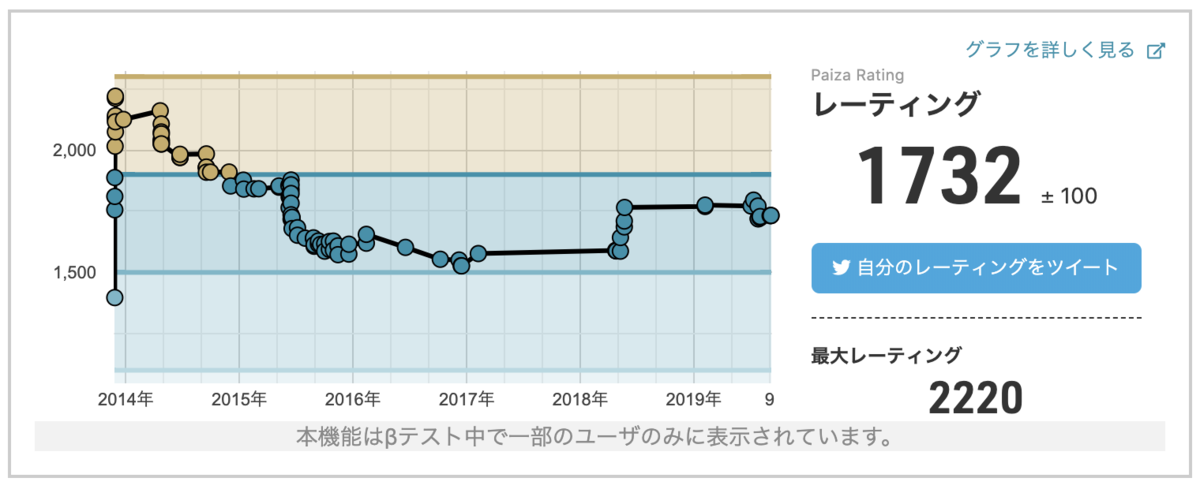
エンジニア戦闘力
「レーティング」として表示
レーティング

エンジニア戦闘力・レーティングの数字

エンジニア戦闘力は100から、レーティングは700から始まります。

問題にも難易度が表示されており、より難易度の高い問題を解けば、エンジニア戦闘力・レーティングも大きく上がります。 逆に、今のエンジニア戦闘力・レーティングよりも簡単な問題が解けないと下がります。

エンジニア戦闘力・レーティングの計算方法

エンジニア戦闘力・レーティングと勝率

エンジニア戦闘力・レーティングの計算では、 問題が解けた場合を「ユーザが問題に勝った」問題が解けない場合を「ユーザが問題に負けた」と考えます。

エンジニア戦闘力が2倍違えば2倍の確率で、10倍違えば10倍の確率で勝てる(＝解ける)と考えます。

たとえば、戦闘力100の人が難易度200の問題に挑戦すると「1勝2敗(1回解けて2回解けない)」、戦闘力100の人が難易度1000の問題に挑戦すると「1勝10敗(1回解けて10回解けない)」と考えます。

戦闘力が10倍違う人がプログラミングで勝負すると、普通は強い人が勝ちますが、約10回に1回は逆転できる 、とも考えられます。

式にすると以下のようになります。これはBradley-Terryモデルとも呼ばれています。

$勝率 = \frac{自分の戦闘力}{自分の戦闘力 + 問題の戦闘力(難易度)}$

勝ちと負けの比(オッズ)であらわすと以下になります。

$オッズ(勝ち負け比) = \frac{自分の戦闘力}{問題の戦闘力(難易度)}$

また、レーティングはエンジニア戦闘力の対数をとります。エンジニア戦闘力は比が10倍あると「10倍の確率で勝てる」のに対して、 レーティングは差が400あると「10倍の確率で勝てる」となります。

「エンジニア戦闘力・レーティング」の更新

戦いが終わる(問題への挑戦が終わる)と、エンジニア戦闘力・レーティングが更新されます。問題を解けば戦闘力はどんどん上がりますが、解けないと戦闘力は下がります。

問題側の視点で考えると、問題が解かれると負けと考えて難易度が下がり、解かれないと勝ちと考えて難易度を上げます。

エンジニア戦闘力とレーティングの関係

エンジニア戦闘力は、スキルに応じて指数的に大きくなりますが、レーティングは線形で大きくなります。

エンジニア戦闘力とレーティングの関係は以下の通りです。

$エンジニア戦闘力 = 10^{(レーティング + 100) / 400}$

$レーティング = (\log_{10} エンジニア戦闘力) \cdot 400 - 100$

表にすると以下になります。

レーティング	エンジニア戦闘力
700 (初期値)	100 (初期値)
1100	1,000
1500	10,000
1900	100,000

Glickoレーティングについて

戦闘力の比が勝率の比になるので、式で表すと以下のようになります。たとえば戦闘力比が2の場合、勝率は2/3ですね。

$勝率 = \frac{戦闘力比}{1 + 戦闘力比}$

これをグラフにすると以下になります。

f:id:paiza:20190905173037p:plain — 戦闘力比 - 勝率

x = np.linspace(0, 100, 100)
y = x/(1+x)
plt.grid()
plt.xlabel("戦闘力比")
plt.ylabel("勝率")
plt.plot(x, y)

戦闘力は範囲が広いので、レーティングでは戦闘力の対数をとります。

この場合、勝率は以下のようにレーティング差から求められます。

$勝率 = \frac{10^{レーティング差 / 400}}{ 1 + 10^{レーティング差 / 400}}$

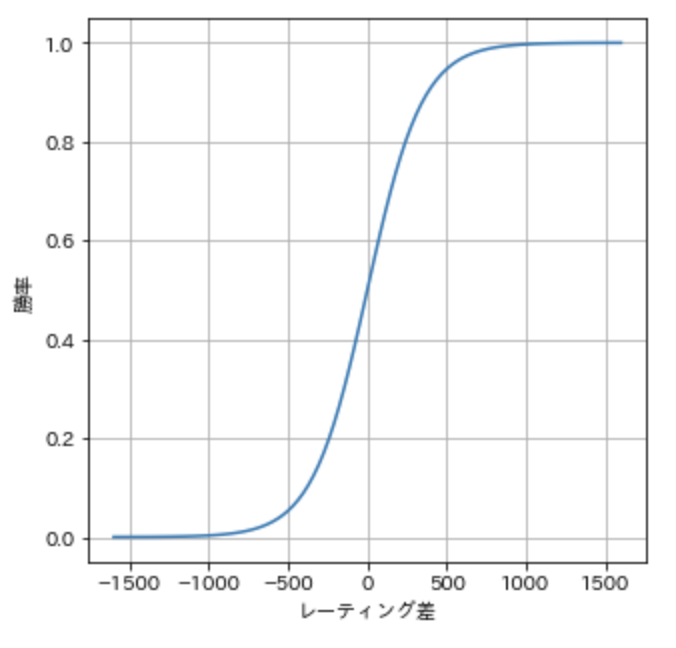
これは、以下のような勝率50%を中心とした左右対称のグラフになります。ロジスティック関数やシグモイド関数とも呼ばれています。

f:id:paiza:20190910134711p:plain — レーティング差 - 勝率グラフ

x = np.linspace(-1600, 1600, 100)
y = 10**(x/400) / (1 + 10**(x/400))
plt.grid()
plt.xlabel("レーティング差")
plt.ylabel("勝率")
plt.plot(x, y)

レーティング(戦闘力の対数)を求めるには、勝ち負け(問題が解けたかどうか)の結果から、このロジスティック関数での勝率50%の場所を求めることになります。

全ユーザと全問題について、スキルチェックのチャレンジ結果から項目応答理論のようにロジスティック回帰(EM法など)を用いて推定することもできますが、問題を解くたびに全てを計算し直すと大変ですし、解いた問題が少ないとうまく収束させることが難しくなってきます。

そこで、 Glickoレーティングを利用します。

Glickoレーティングとは、チェスの大会でレーティングを求めるために考えられた方法で、スプラトゥーンのレーティングなどでも使われています。

Glickoレーティングは、もともと同時に多数のユーザーがゲームをした場合を想定していますが、今回は問題に挑戦することを「ユーザーと問題が対戦した」、問題が解けたことを「ユーザーが問題に勝った」と考えて計算してみます。

Glickoレーティングでは、各ユーザーは以下の数字を持ち、レーティング(戦闘力の対数)は対戦ごとに逐次更新します。

レーティング(戦闘力の対数)：初期値1500。
RD(レーティング偏差)：レーティングの正確さをあらわす。初期値350。

レーティング差400で、プレイヤーの能力が10倍になるようにします。

多くの問題を解いたユーザーや、多くの人に解かれた問題のレーティングはより正確なものになっていきますが、ほとんど問題を解いていないユーザーや、解かれていない問題のレーティングはあまり正確なものではありません。レーティングが確率的に正規分布していると考えて、正確さをRDで表します。

RDの大きい(＝不正確)なユーザが、RDの小さい(＝正確)問題を解いた場合、ユーザーのレーティングは大きく変わりますが、問題のレーティングはあまり変わりません。

Glickoレーティングの計算式

レーティングの計算式は、以下になります。(1つの大会で1ゲームのみという場合)

自分のレーティング、レーティング偏差: r, RD

相手のレーティング、レーティング偏差: $r_1, RD_1$

対戦結果: s (勝ち=1, 負け=0)

レーティングの更新式:

$r' = r + q \cdot RD'^{2} \cdot g(RD_1) \cdot (s - E)$

レーティング偏差の更新式:

$RD' = \frac{1}{\sqrt{ \frac{1}{RD^2} + \frac{1}{d^2} }}$

勝率の精度:

$g(RD) = \frac{1}{\sqrt{1 + \frac{3}{π^2} \cdot q \cdot RD^{2} }}$

勝率:

$E = \frac{1}{ 1 + 10^{g(RD1) \cdot (r-r_1)} }$

尤度の分散:

$d^2 = \frac{1}{q^2 \cdot g(RD_1)^2 \cdot E \cdot (1-E)}$

係数:

$q = \frac{log 10}{400}$

Glickoレーティングの計算式の導出

上記の式さえあればレーティングは計算できますが、そもそもどうやってこの式が出てきたのか考えてみましょう。

ここではレーティングを簡略化し、勝率(s=1)と負ける確率(s=0)が以下のように表せるとします。

$E(r, r_1, s) = \frac{e^{(r-r_1) \cdot s}}{1 + e^{r-r_1}}$

ここから、結果がsの時にレーティング(パラメータ/母数)がr, $r_1$ となる尤もらしさを表す「尤度関数」と考えて、以下のように書き換えます。

$L(r, r_1 | s) = E(r, r_1, s)$

相手のレーティングと積分すると、 $r_1$ が消えて周辺尤度関数は以下のように表せます。対戦相手の事後分布ではなく、事前分布を使うことで計算を簡略化しています。ここでφは標準正規分布の確率密度関数です。

$L(θ|s) = \int E(θ, θ_1, s) \cdot φ(θ_1 | r_1, rd_1^2) dθ_1$

ここで正規分布とロジスティック分布が類似していて、標準ロジスティック関数の分散が π² / 3 であることを利用すると、以下になります。

$L(θ|s) = \frac{10^{g \cdot (θ - r_1) \cdot s }}{1 + 10^{g \cdot (θ - r_1)} }$

対数をとると以下になります。

$log L(θ|s) = g \cdot s \cdot (θ - r_1) - log ( 1 + 10^{g \cdot (θ - r_1)} )$

レーティング(θ)を最尤推定(MAP推定)で推定するため、対数尤度を微分して0になる時点のレーティング ( $\hat{r}$ ) を探します。

$\frac{d}{dθ} log L(\hat{r} | s) = g \cdot (s - \frac{1}{1 + 10^{-g \cdot (\hat{r} - r_1)}}) = 0$

また、尤度関数を2回微分してフィッシャー情報量を求めます。

$I(θ) = - \frac{d^2}{dθ^2} log (L(θ | s)) \\ = g^2 \cdot E(r^, θ, rd_1, s) \cdot (1 - E(θ, r_1, rd_1, ))$

このフィッシャー情報量の逆数をとって、レーティング(観測分布/尤度)の分散を求めます。

$d^2 = \frac{1}{I(\hat{r})} = \frac{1}{ g^2 \cdot E(\hat{r}) \cdot (1 - E(\hat{r})) }$

レーティングの事後分布は、事前分布と観測分布(尤度関数)の積なので以下のようになります。

$f(θ|s) = φ(θ | r, rd^2) \cdot L(θ | s)$

尤度も正規分布で近似すると、事後分布は以下のようになります。

$f(θ|s) = φ(θ | r, rd^2) \cdot φ(θ | \hat{r}, d^2)$

事前分布がN(r, rd²)、観測分布がN(r^, d²)の時の事後分布N(r', rd')なので、逐次ベイズ推定(カルマンフィルタ)により、事後分布は以下のようにして求められます。

分散:

$rd'^2 = \frac{1}{\frac{1}{r^2} + \frac{1}{d^2}}$

平均:

$r' = rd' * ( \frac{r}{rd^2} + \frac{\hat{r}}{d^2} ) \\ = r + \frac{rd'^2}{d^2} \cdot (\hat{r} - r)$

観測分布は勝率を線形近似して求めます。

$h(r) = \frac{g}{1 + e^{-g * (r - r_1)}}$

とすると

$h(\hat{r}) = g \cdot s$

$h(\hat{r}) = h(r) + (\hat{θ} - r) * h'(r)$

なので、事後分布の平均の更新は、以下の通りです。

$r' = r + \frac{rd'^2}{d^2} \cdot \frac{h(\hat{θ}) - h(r)}{h'(r)} \\ = r + rd'^2 \cdot (h(\hat{θ}) - h(r)) \\ = r + rd'^2 \cdot g \cdot (s - E) \\$

上記をまとめると、以下のようになります。

$r' = r + rd'^2 \cdot g \cdot (s - E) \\ rd' = \frac{1}{\sqrt{\frac{1}{rd^2} + \frac{1}{d^2}}} \\ g = \frac{1}{\sqrt{1 + \frac{3}{π^2} \cdot rd^2}} \\ E = \frac{1}{1 + e^{g * (r - r1)}} \\ d^2 = g^2 \cdot E \cdot (1-E)$

これをレーティング差400が勝率10倍になるように調整すると、Glickoレーティングの計算式になります。

スキルチェック向けのGlickoレーティングのパラメータ設定

もともとのGlickoレーティングでは、(上の式では出ていませんが)大会の間隔が広いとレーティングが不正確になると考えて、RDを大きくします。

今回は、プログラミング力について、問題を解いた間隔による影響がわからないので、この調整はおこなっていません。

そのかわり、ユーザーのレーティングについて、RDの最小値を100にして、レーティングが固定されてしまうことを防いでいます。

また、Glickoレーティングの初期値は1500(中程度の強さ)となっていますが、スキルチェックにおいてプログラミング力が不明な場合に「中程度のスキルがある」とするのは適切ではないですよね。そのため、初期レーティングは一番簡単な問題と同じ700にしています。

ユーザの初期レーティングを700と低くした状態で、そのまま問題のレーティングを求めると、問題のレーティングも下がってしまいます。そこで、ユーザーのレーティングは、問題レーティングの計算に利用する内部レーティング(初期値1500)と、表示用の外部レーティング(初期値700)に分け、外部レーティングの計算時は問題レーティングを更新しないようにします。

パラメータについては調整の余地があると思いますので、データを見ながら適時調整したいと考えています。

他のレーティングシステムについて

レーティングシステム、今回用いたGlickoレーティング以外にもいろいろあります。

Glicko-2 Glickoレーティングを発展させたもので、レーティングのブレやすさが考慮されています。これにより、そのユーザーの「気まぐれさ」まで考慮できます。ただ、スキルチェックでは、ユーザーと問題の1回の対戦のみで更新するため、Glicko-2は有効に機能しません。
TrueSkill マイクロソフトが開発したレーティングシステムです。1対1の対戦以外などでも利用できます。

レーティング計算の例

実際にどのようにレーティングが計算されるかの例を見てみましょう。paiza.IOを使って計算してみました。

例1

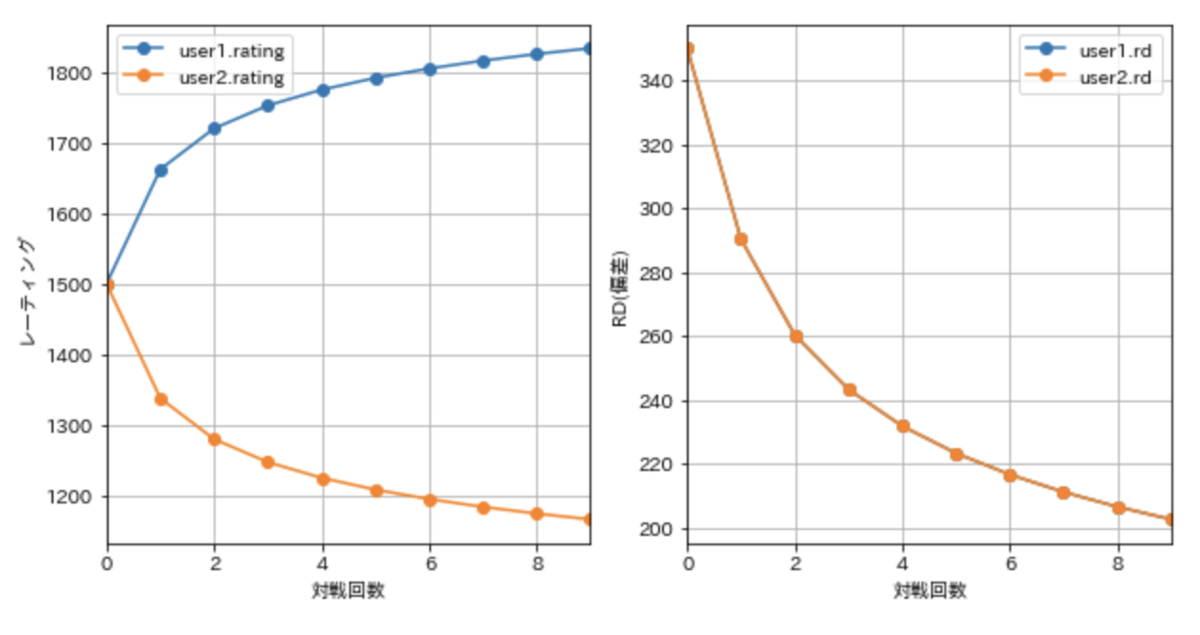
ユーザ初期値: レーティング=1500, RD=350

問題初期値: レーティング=1500, RD=350

この状態で、10回連続でユーザが問題に勝った(＝解けた)場合のユーザーと問題のレーティングの推移グラフです。

f:id:paiza:20190910141032p:plain — レーティング推移

df = pd.DataFrame(data, columns=('user1.rating', 'user2.rating', 'user1.rd', 'user2.rd'))
fig, axes = plt.subplots(nrows=1, ncols=2)

axes[0].set_xlabel('対戦回数')
axes[0].set_ylabel('レーティング')
df.plot(ax=axes[0] , y=['user1.rating', 'user2.rating'], marker='o', grid=True)

axes[1].set_xlabel('対戦回数')
axes[1].set_ylabel('RD(偏差)')
df.plot(ax=axes[1] , y=['user1.rd', 'user2.rd'], marker='o', grid=True)

例2

ユーザ初期値: レーティング=1500, RD=350

問題初期値: レーティング=1500, RD=100

今度は、問題のRD(偏差)を100と小さくしてみます。この場合、RDが大きいユーザのレーティングは大きく変わりますが、RDの小さい問題のレーティングはあまり変わりません。

f:id:paiza:20190910142043p:plain — レーティングの推移

正確さの確認

レーティングは計算できたので、実際にレーティングがユーザーのスキルを正しく表しているかを確認してみましょう。

ランクとの関係

まずは、レーティングとランクとの関係を見てみましょう。横軸がレーティング、縦軸が人数です。

レーティングとランクが相関していることがわかりますよね。また、同じランクの人たちでもレーティングには幅があることがわかります。

f:id:paiza:20190906184415p:plain — レーティングとランクの関係

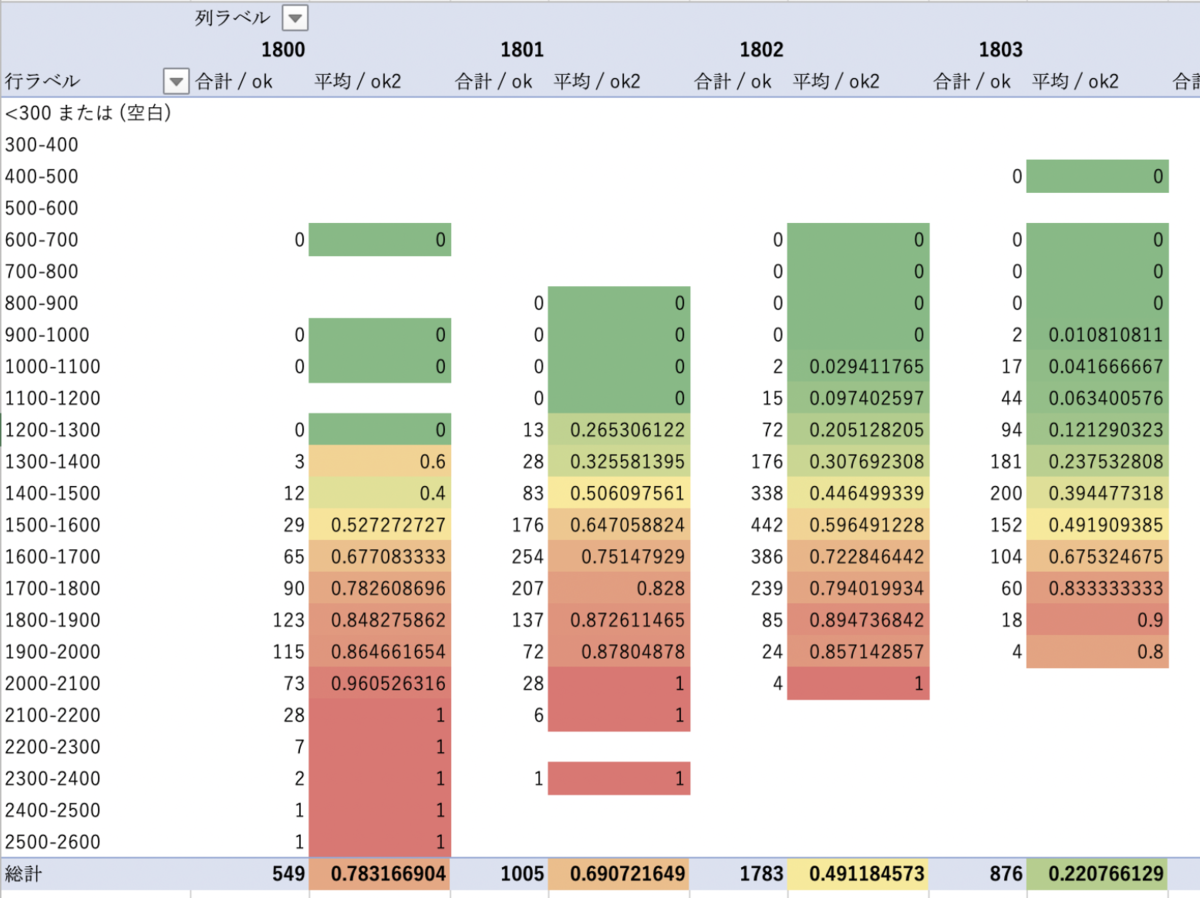
問題の正解率

レーティングとランク別の、ある問題(C056:テストの採点(id:266) )の正解率を見てみましょう。横軸がランク、縦軸がレーティング、数字と色が正解率になります。

同じ行を見ると、ランクが違っても同じレーティングの場合は正解率が近いことがわかります。一方で、同じ列を見ると同じランクでもレーティングが違うと正解率が変わってきます。レーティングの方が、より正確に正解率を表していると考えられます。

f:id:paiza:20190905183452p:plain

問題の正答率

各問題について、ユーザのレーティングと正答率の関係を見てみましょう。また、ロジスティック回帰を行い、正答率がロジスティック分布になっているか確認していみます。

横軸をユーザのレーティング、縦軸が正答率です。

オレンジ色の折れ線が正答率、青色の曲線がロジスティック回帰の結果、青の縦棒が問題のレーティングになります。

f:id:paiza:20190906155543p:plain — D022:表面積の計算

f:id:paiza:20190906155701p:plain — C016:Leet文字列

f:id:paiza:20190906155805p:plain — B021:複数形への変換

f:id:paiza:20190906155910p:plain — A017:落ちものシミュレーション

f:id:paiza:20190906160055p:plain — S015:ABC文字列

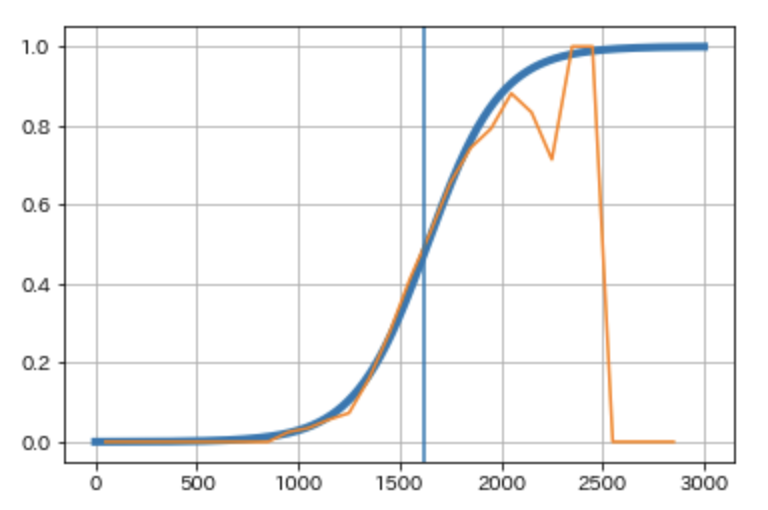
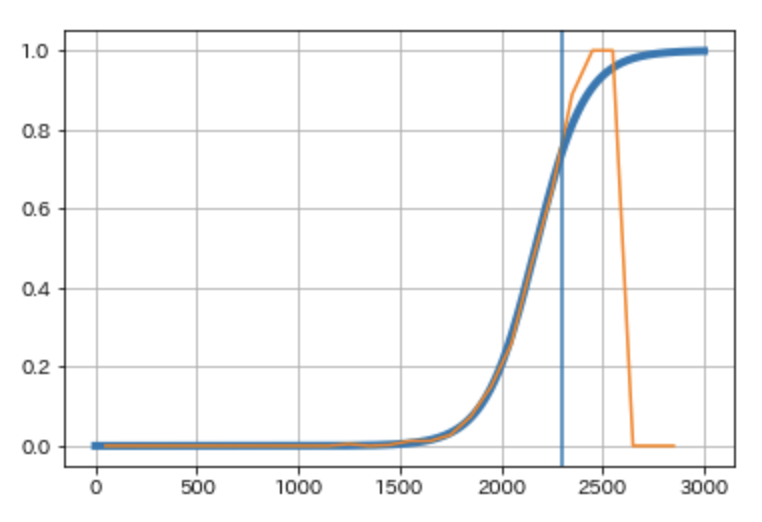
レーティングは、問題の正答率がレーティングに対するロジスティック関数となることを想定していますが、およそロジスティック関数に一致していることから、モデルが正しいと考えられます。ただ、問題のよって曲線の傾きが異なり、例えば以下の問題では傾きがゆるくなっています。

f:id:paiza:20190906162544p:plain — D034:どれにしようかな

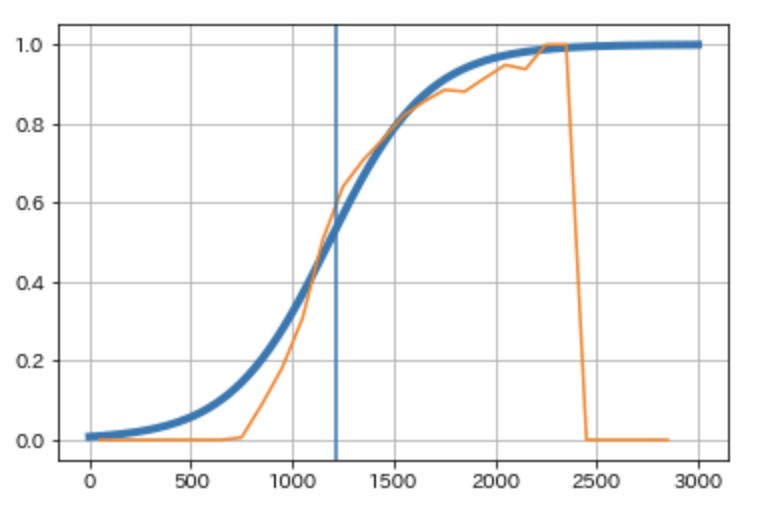
あまりに問題の傾きがゆるやかな場合はプログラミング以外の能力が関連している可能性や、そもそも問題がわかりにくい可能性もありますので、改善を検討することができます。

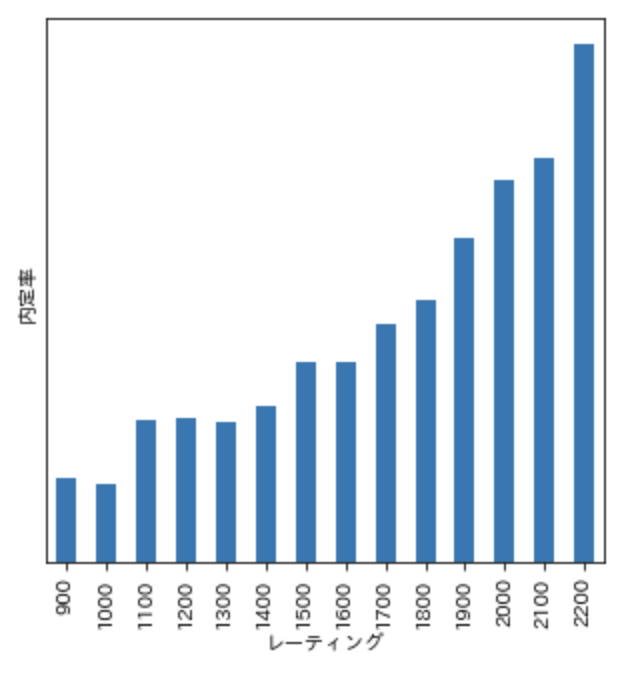
レーティングと内定率の関係

レーティングと内定率の関連を見てみましょう。横軸がレーティングで、縦軸が内定率になります。レーティングが高いほど内定率も上がっています。レーティングがユーザーのスキルと関連していて、スキルが高いほど内定が得やすいと考えられます。

f:id:paiza:20190909160236p:plain — レーティング-内定率グラフ

レーティングと年収の関係

レーティングと内定年収の関係を見てみましょう。横軸がレーティングで、縦軸が年収です。ぱっと見ても、レーティング(横)が上がる(右になる)ほど年収が上がっているのがわかります。レーティングが高いほどスキルが高く、年収も高くなっていると考えられます。

f:id:paiza:20190910151607p:plain — レーティング - 内定年収グラフ

参考

Welcome to Glicko ratings
The Glicko system
Parameter estimation in large dynamic paired comparison experiments
正規分布の事後分布の平均と分散【ベイズ】 | AVILEN AI Trend
シンプルなモデルとイラストでカルマンフィルタを直観的に理解してみる - Qiita
基礎統計学III(ブラッドリーテリー(Bradley-Terry’s) model, p. 167)
基礎統計学II(ロジスティック関数での最尤推定のフィッシャー情報量/項目情報関数, p. 345)

まとめ

paizaでスキルチェック問題を解いた経験のある方は、ぜひ他の問題も解いてみることで、ご自分の「エンジニア戦闘力」「レーティング」がどう変わっていくか試してみてください。

スキルチェック問題について、詳しくはこちら

なお、上記はユーザーによって表示される内容が変わり、また効果やメリットについても検証中のため、表示形式は適宜変更されていきます。

「PaizaCloud」は、環境構築に悩まされることなく、ブラウザだけで簡単にウェブサービスやサーバアプリケーションの開発や公開ができます。

「paizaラーニング」では、未経験者でもブラウザさえあれば、今すぐプログラミングの基礎が動画で学べるレッスンを多数公開しております。

そして、paizaでは、Webサービス開発企業などで求められるコーディング力や、テストケースを想定する力などが問われるプログラミングスキルチェック問題も提供しています。

スキルチェックに挑戦した人は、その結果によってS・A・B・C・D・Eの6段階のランクを取得できます。必要なスキルランクを取得すれば、書類選考なしで企業の求人に応募することも可能です。「自分のプログラミングスキルを客観的に知りたい」「スキルを使って転職したい」という方は、ぜひチャレンジしてみてください。