paizaでは、先日「8月13日はpaizaの日!怪盗813からの挑戦状プレゼントキャンペーン」を実施いたしました。
たくさんの方にご挑戦いただきまして、ありがとうございます!
今回は、こちらの問題の解説をします。(※コードは全てJavaで解説しております)
※プレゼント当選者の方へのAmazonギフト券・松阪牛の発送が遅れており大変申し訳ございませんが、順次発送を予定しております!
■怪盗813からの挑戦状・解説
まず怪盗813からの挑戦状ですが、問題は
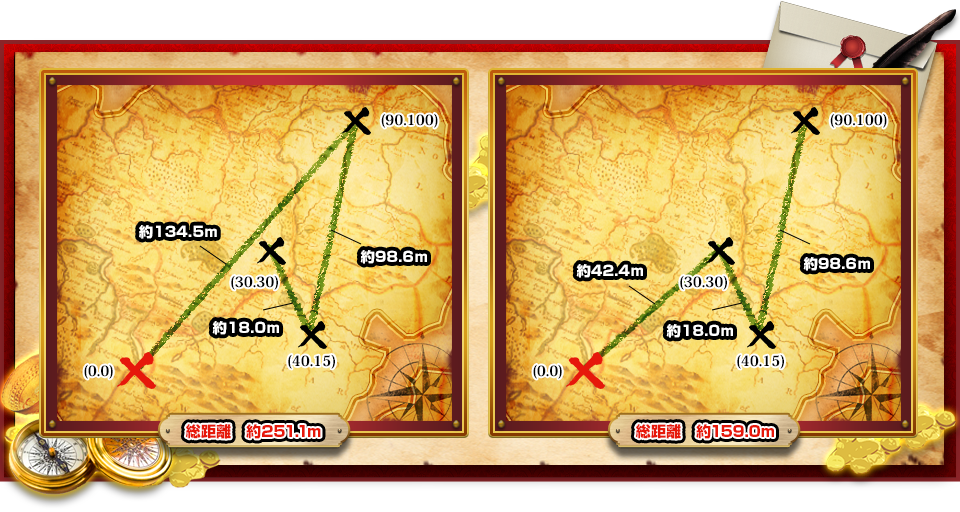
怪盗からお宝の場所の情報が届きました。お宝のある場所の情報のみでルートなどは分かっていません。 お宝の場所の情報は怪盗の居る場所を 0, 0 として N 個 のお宝の x, y 座標がメートル単位で書かれています。 各座標間は直線で移動します。 0, 0 の位置からスタートし、可能な限り短いルートでお宝を全て盗むルートを出力してください。 必ず最短距離である必要はありません。 以下の図は入力例1 の2パターンを表したものです。
上記2パターンはどちらも正解となりますが右の総距離 159.0 m のルートの方が短く良いルートとジャッジされます。
入力される値
入力は以下のフォーマットで与えられます。N (N はお宝の総数)
x_1 y_1 (x_1 は 1 個目のお宝の場所の x 座標、 y_1 は 1 個目のお宝の場所の y 座標)
x_1 y_1 (x_2 は 2 個目のお宝の場所の x 座標、 y_2 は 2 個目のお宝の場所の y 座標)
・・・
x_N y_N (x_N は N 個目のお宝の場所の x 座標、 y_N は N 個目のお宝の場所の y 座標)
条件
・全ての値は整数
・1 ≦ N ≦ 100
・1 ≦ x_i, y_i ≦ 1000000 (1 ≦ i ≦ N)
期待する出力
お宝を全てゲットできるルートを出力して下さい。
最後は改行し、余計な文字、空行を含んではいけません。
入力例1
3
90 100
40 15
30 30
入力例2
5
1 1
40 120
199 256
10 30
50 5
出力例1
90 100
40 15
30 30
出力例2
1 1
40 120
199 256
10 30
50 5
この問題は、効率的に全てのお宝がゲットできるルートを出力する、「巡回セールスマン問題」と呼ばれるものです。
ただしこの問題の場合、スタート地点が0, 0で固定されている点や、最後は元の位置に戻ってこなければならない点などが、一般的な巡回セールスマン問題とは少し異なっています。
まずはアルゴリズム等を考えず、とにかく答えとして成立する出力をしてみる場合ですが……最短経路を求めず、とりあえず入力があった順に座標を出力してみましょう。
一応これでもルートとしては成立しているので、不正解とはならず点数はつきます。
これではさすがにそのまますぎるので、例えば「0, 0に近い順で回るとよいのでは?」という考え方で、x, y座標を小さい順に並べる…みたいな処理を入れた方もいるかもしれませんね。
しかし、それだけではきちんと効率的なルートを計算できているわけではないので、あまり良い点にはなりません。
では、「全ての経路を総当たりで探して一番近いものを選ぶ」という方法を考えてみましょう。
すべての経路を探すとなると……N箇所のお宝の位置を順に全てチェックしていくため、計算量は O(N!) となります。
5箇所程度であれば120パターンなので、それぐらいなら全ルートを調べられるかもしれませんが、10箇所となると3628800パターン、100箇所となると93326215443944152681……省略しますが、156桁の数分のパターンを出して最短経路を探さねばならず、現実的ではありません。
もっと現実的な解法を考えてみましょう。近似解の距離を元にした貪欲法が以下になります。
<参考>
近似アルゴリズム - Wikipedia
貪欲法 - Wikipedia
この場合、まず0,0から距離の近い地点を探す→その地点から一番近い地点を探す→その地点から一番近い地点を……と言う感じで、距離をもとに現在値から近いところを巡っていく……という解き方になっています。
この解き方については、paizaラーニングの無料講座「アルゴリズム入門編: 「巡回セールスマン問題」を学ぶ」でも解説しています。
→アルゴリズム入門編: 「巡回セールスマン問題」を学ぶのチャプター一覧 | プログラミング学習サービス【paizaラーニング】
貪欲法は一見効率的に思えますが、入力データによっては最終的にものすごく遠回りなルートになってしまうケースもあり得ます。戻るときの距離が考慮されていないからですね。現在値から近い点をひたすら辿るだけだと、どんどん遠くへ行ってしまい、最後に戻るときのの距離がとんでもないことになってしまうとか……。この貪欲法に処理をいろいろ加えて改善していくと、もっと効率的になっていくかと思います。
実際に、ランキング上位に入った解答では焼きなまし法やビームサーチを使った解き方などがありました。ほかにも遺伝的アルゴリズムを使った解き方や、2-opt、クリストフィードのアルゴリズム、最小全域木を使った近似……などなど、本当~にいろいろなアルゴリズムを使った解き方ができます。粘菌を使ったアルゴリズムなんてのもあります。
興味のある方は、いろいろなアルゴリズムで解いて試してみると楽しいかもしれません。
<参考>
焼きなまし法 - Wikipedia
遺伝的アルゴリズム - Wikipedia
クリストフィードのアルゴリズム - Wikipedia
全域木 - Wikipedia
アルゴリズムに詳しくない初心者の方は、まず貪欲法を理解して、そこからどうやって工夫するとよりよくなりそうか?ということを考えてみるのがよいかと思います。
詳しくは「アルゴリズム入門編: 「巡回セールスマン問題」を学ぶ」をごらんください!
→アルゴリズム入門編: 「巡回セールスマン問題」を学ぶのチャプター一覧 | プログラミング学習サービス【paizaラーニング】
■おまけ
これは完全に運任せのギャンブル解法です。ランダムに配列を並び替えて、距離が短くなったら更新……を何度か繰り返し、最終的な結果を出力します。
上記のコードでは、1000000回配列を並び替えて良い結果を出しています。
この解法を何度も何度も提出していれば、いつかは1位を取れる日が来るかも……?と言いたいところですが、確率は1000000/100!なので、現実的にはめちゃくちゃ難しいですね……。でも、解き方の一つとしては面白いですね。
■Railsの有料講座を限定無料公開中!動画で学べるpaizaラーニング
「アルゴリズム入門編: 「巡回セールスマン問題」を学ぶ」は常に無料公開中の講座ですが、現在「paizaラーニング」では、ふだん有料公開しているRuby on Railsの入門レッスンを、期間限定で連続無料公開しています。paizaラーニングは、動画講座を見たあとに、ブラウザ上で演習問題を解いて、実行結果を見ながら学習を進めていくことができる学習サービスです。
さらに、9月29日(金)までに演習問題の結果をツイートすると、抽選でAmazonギフト券1万円分が1名様、500円分が20名様に当たるキャンペーンも実施しております。
※スケジュールは変更になることがあります。
paizaラーニング無料公開スケジュール・Rails編
| 動画レッスン名 | 無料期間 |
|---|---|
| Rails入門1 | いつでも無料 |
| Rails入門1-2 | 9/15(金)~9/18(月)まで無料 |
| Rails入門1-3 | 9/19(火)~9/21(木)まで無料 |
| Rails入門2 | 9/22(金)~9/25(月)まで無料 |
| Rails入門3 | 9/26(火)~10/1(日)まで無料 |

「paizaラーニング」では、未経験者でもブラウザさえあれば、今すぐプログラミングの基礎が動画で学べるレッスンを多数公開しております。
詳しくはこちら

そして、paizaでは、Webサービス開発企業などで求められるコーディング力や、テストケースを想定する力などが問われるプログラミングスキルチェック問題も提供しています。
スキルチェックに挑戦した人は、その結果によってS・A・B・C・D・Eの6段階のランクを取得できます。必要なスキルランクを取得すれば、書類選考なしで企業の求人に応募することも可能です。「自分のプログラミングスキルを客観的に知りたい」「スキルを使って転職したい」という方は、ぜひチャレンジしてみてください。
詳しくはこちら